Skip to content

867. Transpose Matrix

Description

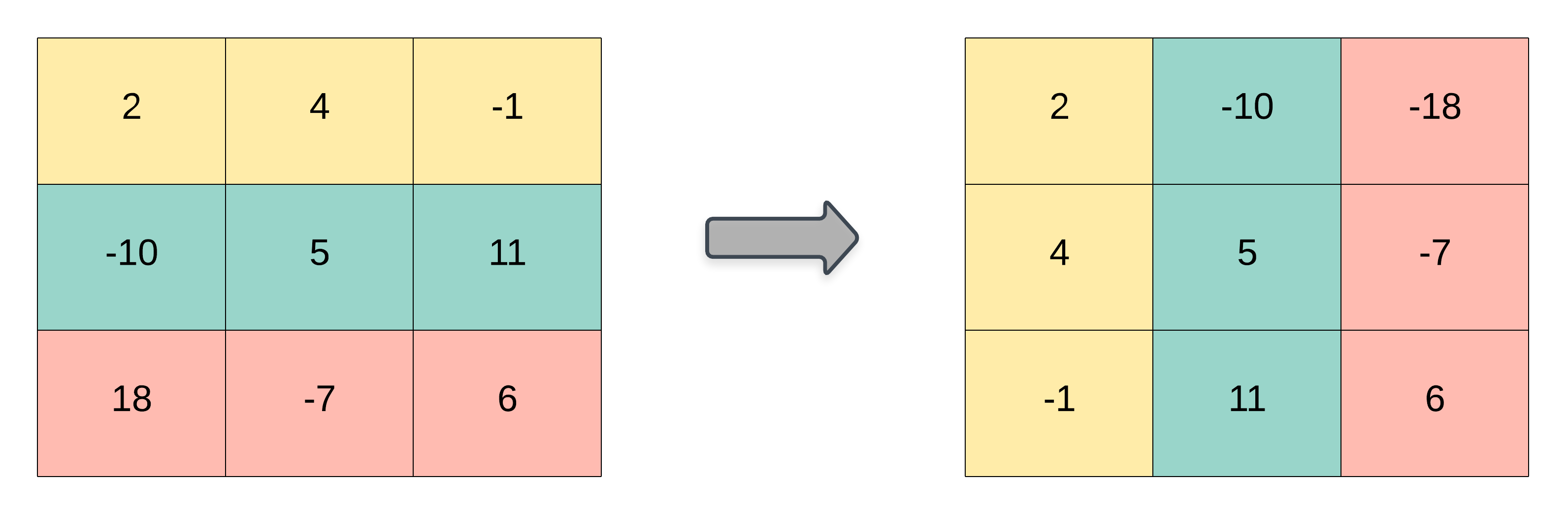
Given a 2D integer array matrix, return the transpose of matrix.

The transpose of a matrix is the matrix flipped over its main diagonal, switching the matrix's row and column indices.

 

Example 1:

Input: matrix = [[1,2,3],[4,5,6],[7,8,9]]
Output: [[1,4,7],[2,5,8],[3,6,9]]

Example 2:

Input: matrix = [[1,2,3],[4,5,6]]
Output: [[1,4],[2,5],[3,6]]

 

Constraints:

  • m == matrix.length
  • n == matrix[i].length
  • 1 <= m, n <= 1000
  • 1 <= m * n <= 105
  • -109 <= matrix[i][j] <= 109

Solutions

Solution 1: Simulation

Let $m$ be the number of rows and $n$ be the number of columns in the matrix $\textit{matrix}$. According to the definition of transpose, the transposed matrix $\textit{ans}$ will have $n$ rows and $m$ columns.

For any position $(i, j)$ in $\textit{ans}$, it corresponds to the position $(j, i)$ in the matrix $\textit{matrix}$. Therefore, we traverse each element in the matrix $\textit{matrix}$ and transpose it to the corresponding position in $\textit{ans}$.

After the traversal, we return $\textit{ans}$.

The time complexity is $O(m \times n)$, where $m$ and $n$ are the number of rows and columns in the matrix $\textit{matrix}$, respectively. Ignoring the space consumption of the answer, the space complexity is $O(1)$.

1
2
3
class Solution:
    def transpose(self, matrix: List[List[int]]) -> List[List[int]]:
        return list(zip(*matrix))

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
class Solution {
    public int[][] transpose(int[][] matrix) {
        int m = matrix.length, n = matrix[0].length;
        int[][] ans = new int[n][m];
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < m; ++j) {
                ans[i][j] = matrix[j][i];
            }
        }
        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
class Solution {
public:
    vector<vector<int>> transpose(vector<vector<int>>& matrix) {
        int m = matrix.size(), n = matrix[0].size();
        vector<vector<int>> ans(n, vector<int>(m));
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < m; ++j) {
                ans[i][j] = matrix[j][i];
            }
        }
        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
func transpose(matrix [][]int) [][]int {
    m, n := len(matrix), len(matrix[0])
    ans := make([][]int, n)
    for i := range ans {
        ans[i] = make([]int, m)
        for j := range ans[i] {
            ans[i][j] = matrix[j][i]
        }
    }
    return ans
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
function transpose(matrix: number[][]): number[][] {
    const [m, n] = [matrix.length, matrix[0].length];
    const ans: number[][] = Array.from({ length: n }, () => Array(m).fill(0));
    for (let i = 0; i < n; ++i) {
        for (let j = 0; j < m; ++j) {
            ans[i][j] = matrix[j][i];
        }
    }
    return ans;
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
/**
 * @param {number[][]} matrix
 * @return {number[][]}
 */
var transpose = function (matrix) {
    const [m, n] = [matrix.length, matrix[0].length];
    const ans = Array.from({ length: n }, () => Array(m).fill(0));
    for (let i = 0; i < n; ++i) {
        for (let j = 0; j < m; ++j) {
            ans[i][j] = matrix[j][i];
        }
    }
    return ans;
};

Comments