Skip to content

864. Shortest Path to Get All Keys

Description

You are given an m x n grid grid where:

  • '.' is an empty cell.
  • '#' is a wall.
  • '@' is the starting point.
  • Lowercase letters represent keys.
  • Uppercase letters represent locks.

You start at the starting point and one move consists of walking one space in one of the four cardinal directions. You cannot walk outside the grid, or walk into a wall.

If you walk over a key, you can pick it up and you cannot walk over a lock unless you have its corresponding key.

For some 1 <= k <= 6, there is exactly one lowercase and one uppercase letter of the first k letters of the English alphabet in the grid. This means that there is exactly one key for each lock, and one lock for each key; and also that the letters used to represent the keys and locks were chosen in the same order as the English alphabet.

Return the lowest number of moves to acquire all keys. If it is impossible, return -1.

 

Example 1:

Input: grid = ["@.a..","###.#","b.A.B"]
Output: 8
Explanation: Note that the goal is to obtain all the keys not to open all the locks.

Example 2:

Input: grid = ["@..aA","..B#.","....b"]
Output: 6

Example 3:

Input: grid = ["@Aa"]
Output: -1

 

Constraints:

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 30
  • grid[i][j] is either an English letter, '.', '#', or '@'. 
  • There is exactly one '@' in the grid.
  • The number of keys in the grid is in the range [1, 6].
  • Each key in the grid is unique.
  • Each key in the grid has a matching lock.

Solutions

Solution 1: State Compression + BFS

According to the problem description, we need to start from the initial position, move in four directions (up, down, left, right), collect all keys, and finally return the minimum number of moves required to collect all keys. If it is not possible to collect all keys, return $-1$.

First, we traverse the 2D grid to find the starting position $(si, sj)$ and count the number of keys $k$.

Then, we can use Breadth-First Search (BFS) to solve this problem. Since the number of keys ranges from $1$ to $6$, we can use a binary number to represent the state of the keys, where the $i$-th bit being $1$ indicates that the $i$-th key has been collected, and $0$ indicates that the $i$-th key has not been collected.

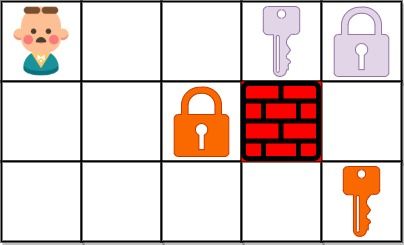
For example, in the following case, there are $4$ bits set to $1$, indicating that keys 'b', 'c', 'd', 'f' have been collected.

1 0 1 1 1 0
^   ^ ^ ^
f   d c b

We define a queue $q$ to store the current position and the state of the collected keys, i.e., $(i, j, \textit{state})$, where $(i, j)$ represents the current position, and $\textit{state}$ represents the state of the collected keys. The $i$-th bit of $\textit{state}$ being $1$ indicates that the $i$-th key has been collected; otherwise, it indicates that the $i$-th key has not been collected.

Additionally, we define a hash table or array $vis$ to record whether the current position and the state of the collected keys have been visited. If visited, there is no need to visit again. $vis[i][j][\textit{state}]$ indicates whether the position $(i, j)$ and the state of the collected keys $state$ have been visited.

We start from the initial position $(si, sj)$, add it to the queue $q$, and set $vis[si][sj][0]$ to $true$, indicating that the initial position and the state of the collected keys $0$ have been visited.

During the BFS process, we take out a position $(i, j, \textit{state})$ from the front of the queue and check whether the current position is the endpoint, i.e., whether the current position has collected all keys, which means the number of $1$s in the binary representation of $state$ is $k$. If so, we return the current number of steps as the answer.

Otherwise, we move from the current position in four directions (up, down, left, right). If we can move to the next position $(x, y)$, we add $(x, y, nxt)$ to the queue $q$, where $nxt$ represents the state of the keys at the next position.

Here, $(x, y)$ must first be within the grid range, i.e., $0 \leq x < m$ and $0 \leq y < n$. Secondly, if the position $(x, y)$ is a wall, i.e., grid[x][y] == '#', or the position $(x, y)$ is a lock but we do not have the corresponding key, i.e., grid[x][y] >= 'A' && grid[x][y] <= 'F' && (state >> (grid[x][y] - 'A') & 1) == 0), then we cannot move to the position $(x, y). Otherwise, we can move to the position $(x, y).

If the search ends and we have not collected all keys, return $-1$.

The time complexity is $O(m \times n \times 2^k)$, and the space complexity is $O(m \times n \times 2^k)$. Here, $m$ and $n$ are the number of rows and columns of the grid, respectively, and $k$ is the number of keys.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class Solution:
    def shortestPathAllKeys(self, grid: List[str]) -> int:
        m, n = len(grid), len(grid[0])
        # Find the starting point (si, sj)
        si, sj = next((i, j) for i in range(m) for j in range(n) if grid[i][j] == '@')
        # Count the number of keys
        k = sum(v.islower() for row in grid for v in row)
        dirs = (-1, 0, 1, 0, -1)
        q = deque([(si, sj, 0)])
        vis = {(si, sj, 0)}
        ans = 0
        while q:
            for _ in range(len(q)):
                i, j, state = q.popleft()
                # If all keys are found, return the current step count
                if state == (1 << k) - 1:
                    return ans

                # Search in the four directions
                for a, b in pairwise(dirs):
                    x, y = i + a, j + b
                    nxt = state
                    # Within boundary limits
                    if 0 <= x < m and 0 <= y < n:
                        c = grid[x][y]
                        # It's a wall, or it's a lock but we don't have the key for it
                        if (
                            c == '#'
                            or c.isupper()
                            and (state & (1 << (ord(c) - ord('A')))) == 0
                        ):
                            continue
                        # It's a key
                        if c.islower():
                            # Update the state
                            nxt |= 1 << (ord(c) - ord('a'))
                        # If this state has not been visited, enqueue it
                        if (x, y, nxt) not in vis:
                            vis.add((x, y, nxt))
                            q.append((x, y, nxt))
            # Increment the step count
            ans += 1
        return -1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
class Solution {
    private int[] dirs = {-1, 0, 1, 0, -1};

    public int shortestPathAllKeys(String[] grid) {
        int m = grid.length, n = grid[0].length();
        int k = 0;
        int si = 0, sj = 0;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                char c = grid[i].charAt(j);
                if (Character.isLowerCase(c)) {
                    // Count the number of keys
                    ++k;
                } else if (c == '@') {
                    // Starting point
                    si = i;
                    sj = j;
                }
            }
        }
        Deque<int[]> q = new ArrayDeque<>();
        q.offer(new int[] {si, sj, 0});
        boolean[][][] vis = new boolean[m][n][1 << k];
        vis[si][sj][0] = true;
        int ans = 0;
        while (!q.isEmpty()) {
            for (int t = q.size(); t > 0; --t) {
                var p = q.poll();
                int i = p[0], j = p[1], state = p[2];
                // If all keys are found, return the current step count
                if (state == (1 << k) - 1) {
                    return ans;
                }
                // Search in the four directions
                for (int h = 0; h < 4; ++h) {
                    int x = i + dirs[h], y = j + dirs[h + 1];
                    // Within boundary limits
                    if (x >= 0 && x < m && y >= 0 && y < n) {
                        char c = grid[x].charAt(y);
                        // It's a wall, or it's a lock without the corresponding key
                        if (c == '#'
                            || (Character.isUpperCase(c) && ((state >> (c - 'A')) & 1) == 0)) {
                            continue;
                        }
                        int nxt = state;
                        // If it's a key
                        if (Character.isLowerCase(c)) {
                            // Update the state
                            nxt |= 1 << (c - 'a');
                        }
                        // If this state has not been visited, enqueue it
                        if (!vis[x][y][nxt]) {
                            vis[x][y][nxt] = true;
                            q.offer(new int[] {x, y, nxt});
                        }
                    }
                }
            }
            // Increment the step count
            ++ans;
        }
        return -1;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
class Solution {
public:
    const static inline vector<int> dirs = {-1, 0, 1, 0, -1};

    int shortestPathAllKeys(vector<string>& grid) {
        int m = grid.size(), n = grid[0].size();
        int k = 0;
        int si = 0, sj = 0;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                char c = grid[i][j];
                // Count the number of keys
                if (islower(c)) ++k;
                // Starting point
                else if (c == '@')
                    si = i, sj = j;
            }
        }
        queue<tuple<int, int, int>> q{{{si, sj, 0}}};
        vector<vector<vector<bool>>> vis(m, vector<vector<bool>>(n, vector<bool>(1 << k)));
        vis[si][sj][0] = true;
        int ans = 0;
        while (!q.empty()) {
            for (int t = q.size(); t; --t) {
                auto [i, j, state] = q.front();
                q.pop();
                // If all keys are found, return the current step count
                if (state == (1 << k) - 1) return ans;
                // Search in the four directions
                for (int h = 0; h < 4; ++h) {
                    int x = i + dirs[h], y = j + dirs[h + 1];
                    // Within boundary limits
                    if (x >= 0 && x < m && y >= 0 && y < n) {
                        char c = grid[x][y];
                        // It's a wall, or it's a lock without the corresponding key
                        if (c == '#' || (isupper(c) && (state >> (c - 'A') & 1) == 0)) continue;
                        int nxt = state;
                        // If it's a key, update the state
                        if (islower(c)) nxt |= 1 << (c - 'a');
                        // If this state has not been visited, enqueue it
                        if (!vis[x][y][nxt]) {
                            vis[x][y][nxt] = true;
                            q.push({x, y, nxt});
                        }
                    }
                }
            }
            // Increment the step count
            ++ans;
        }
        return -1;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
func shortestPathAllKeys(grid []string) int {
    m, n := len(grid), len(grid[0])
    var k, si, sj int
    for i, row := range grid {
        for j, c := range row {
            if c >= 'a' && c <= 'z' {
                // Count the number of keys
                k++
            } else if c == '@' {
                // Starting point
                si, sj = i, j
            }
        }
    }
    type tuple struct{ i, j, state int }
    q := []tuple{tuple{si, sj, 0}}
    vis := map[tuple]bool{tuple{si, sj, 0}: true}
    dirs := []int{-1, 0, 1, 0, -1}
    ans := 0
    for len(q) > 0 {
        for t := len(q); t > 0; t-- {
            p := q[0]
            q = q[1:]
            i, j, state := p.i, p.j, p.state
            // If all keys are found, return the current step count
            if state == 1<<k-1 {
                return ans
            }
            // Search in the four directions
            for h := 0; h < 4; h++ {
                x, y := i+dirs[h], j+dirs[h+1]
                // Within boundary limits
                if x >= 0 && x < m && y >= 0 && y < n {
                    c := grid[x][y]
                    // It's a wall, or it's a lock without the corresponding key
                    if c == '#' || (c >= 'A' && c <= 'Z' && (state>>(c-'A')&1 == 0)) {
                        continue
                    }
                    nxt := state
                    // If it's a key, update the state
                    if c >= 'a' && c <= 'z' {
                        nxt |= 1 << (c - 'a')
                    }
                    // If this state has not been visited, enqueue it
                    if !vis[tuple{x, y, nxt}] {
                        vis[tuple{x, y, nxt}] = true
                        q = append(q, tuple{x, y, nxt})
                    }
                }
            }
        }
        // Increment the step count
        ans++
    }
    return -1
}

Comments