Skip to content

849. Maximize Distance to Closest Person

Description

You are given an array representing a row of seats where seats[i] = 1 represents a person sitting in the ith seat, and seats[i] = 0 represents that the ith seat is empty (0-indexed).

There is at least one empty seat, and at least one person sitting.

Alex wants to sit in the seat such that the distance between him and the closest person to him is maximized. 

Return that maximum distance to the closest person.

 

Example 1:

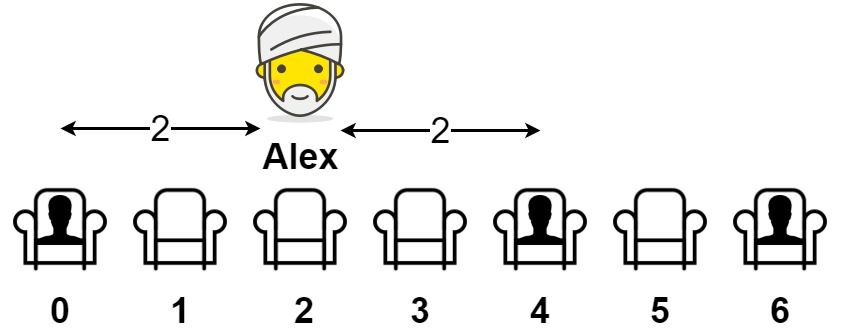
Input: seats = [1,0,0,0,1,0,1]
Output: 2
Explanation: 
If Alex sits in the second open seat (i.e. seats[2]), then the closest person has distance 2.
If Alex sits in any other open seat, the closest person has distance 1.
Thus, the maximum distance to the closest person is 2.

Example 2:

Input: seats = [1,0,0,0]
Output: 3
Explanation: 
If Alex sits in the last seat (i.e. seats[3]), the closest person is 3 seats away.
This is the maximum distance possible, so the answer is 3.

Example 3:

Input: seats = [0,1]
Output: 1

 

Constraints:

  • 2 <= seats.length <= 2 * 104
  • seats[i] is 0 or 1.
  • At least one seat is empty.
  • At least one seat is occupied.

Solutions

Solution 1: Single Traversal

We define two variables $\textit{first}$ and $\textit{last}$ to represent the positions of the first and last person, respectively. We use the variable $d$ to represent the maximum distance between two people.

Then, we traverse the array $\textit{seats}$. If the current position is occupied, and if $\textit{last}$ has been updated before, it means there was someone before, so we update $d = \max(d, i - \textit{last})$. If $\textit{first}$ has not been updated before, it means there was no one before, so we update $\textit{first} = i$. Next, we update $\textit{last} = i$.

Finally, we return $\max(\textit{first}, n - \textit{last} - 1, d / 2)$.

The time complexity is $O(n)$, where $n$ is the length of the array $\textit{seats}$. The space complexity is $O(1)$.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
class Solution:
    def maxDistToClosest(self, seats: List[int]) -> int:
        first = last = None
        d = 0
        for i, c in enumerate(seats):
            if c:
                if last is not None:
                    d = max(d, i - last)
                if first is None:
                    first = i
                last = i
        return max(first, len(seats) - last - 1, d // 2)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
class Solution {
    public int maxDistToClosest(int[] seats) {
        int first = -1, last = -1;
        int d = 0, n = seats.length;
        for (int i = 0; i < n; ++i) {
            if (seats[i] == 1) {
                if (last != -1) {
                    d = Math.max(d, i - last);
                }
                if (first == -1) {
                    first = i;
                }
                last = i;
            }
        }
        return Math.max(d / 2, Math.max(first, n - last - 1));
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int maxDistToClosest(vector<int>& seats) {
        int first = -1, last = -1;
        int d = 0, n = seats.size();
        for (int i = 0; i < n; ++i) {
            if (seats[i] == 1) {
                if (last != -1) {
                    d = max(d, i - last);
                }
                if (first == -1) {
                    first = i;
                }
                last = i;
            }
        }
        return max({d / 2, max(first, n - last - 1)});
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
func maxDistToClosest(seats []int) int {
    first, last := -1, -1
    d := 0
    for i, c := range seats {
        if c == 1 {
            if last != -1 {
                d = max(d, i-last)
            }
            if first == -1 {
                first = i
            }
            last = i
        }
    }
    return max(d/2, max(first, len(seats)-last-1))
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
function maxDistToClosest(seats: number[]): number {
    let first = -1,
        last = -1;
    let d = 0,
        n = seats.length;
    for (let i = 0; i < n; ++i) {
        if (seats[i] === 1) {
            if (last !== -1) {
                d = Math.max(d, i - last);
            }
            if (first === -1) {
                first = i;
            }
            last = i;
        }
    }
    return Math.max(first, n - last - 1, d >> 1);
}

Comments