Skip to content

750. Number Of Corner Rectangles πŸ”’

Description

Given an m x n integer matrix grid where each entry is only 0 or 1, return the number of corner rectangles.

A corner rectangle is four distinct 1's on the grid that forms an axis-aligned rectangle. Note that only the corners need to have the value 1. Also, all four 1's used must be distinct.

 

Example 1:

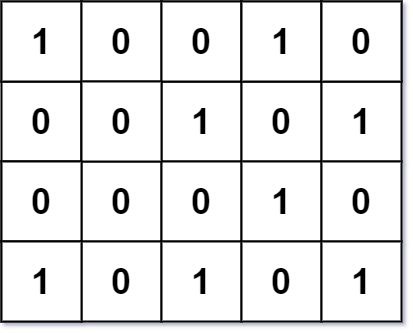
Input: grid = [[1,0,0,1,0],[0,0,1,0,1],[0,0,0,1,0],[1,0,1,0,1]]
Output: 1
Explanation: There is only one corner rectangle, with corners grid[1][2], grid[1][4], grid[3][2], grid[3][4].

Example 2:

Input: grid = [[1,1,1],[1,1,1],[1,1,1]]
Output: 9
Explanation: There are four 2x2 rectangles, four 2x3 and 3x2 rectangles, and one 3x3 rectangle.

Example 3:

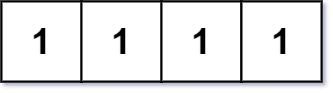
Input: grid = [[1,1,1,1]]
Output: 0
Explanation: Rectangles must have four distinct corners.

 

Constraints:

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 200
  • grid[i][j] is either 0 or 1.
  • The number of 1's in the grid is in the range [1, 6000].

Solutions

Solution 1: Hash Table + Enumeration

We enumerate each row as the bottom of the rectangle. For the current row, if both column $i$ and column $j$ are $1$, then we use a hash table to find out how many of the previous rows have both columns $i$ and $j$ as $1$. This is the number of rectangles with $(i, j)$ as the bottom right corner, and we add this number to the answer. Then we add $(i, j)$ to the hash table and continue to enumerate the next pair $(i, j)$.

The time complexity is $O(m \times n^2)$, and the space complexity is $O(n^2)$. Here, $m$ and $n$ are the number of rows and columns of the matrix, respectively.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
class Solution:
    def countCornerRectangles(self, grid: List[List[int]]) -> int:
        ans = 0
        cnt = Counter()
        n = len(grid[0])
        for row in grid:
            for i, c1 in enumerate(row):
                if c1:
                    for j in range(i + 1, n):
                        if row[j]:
                            ans += cnt[(i, j)]
                            cnt[(i, j)] += 1
        return ans

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public int countCornerRectangles(int[][] grid) {
        int n = grid[0].length;
        int ans = 0;
        Map<List<Integer>, Integer> cnt = new HashMap<>();
        for (var row : grid) {
            for (int i = 0; i < n; ++i) {
                if (row[i] == 1) {
                    for (int j = i + 1; j < n; ++j) {
                        if (row[j] == 1) {
                            List<Integer> t = List.of(i, j);
                            ans += cnt.getOrDefault(t, 0);
                            cnt.merge(t, 1, Integer::sum);
                        }
                    }
                }
            }
        }
        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int countCornerRectangles(vector<vector<int>>& grid) {
        int n = grid[0].size();
        int ans = 0;
        map<pair<int, int>, int> cnt;
        for (auto& row : grid) {
            for (int i = 0; i < n; ++i) {
                if (row[i]) {
                    for (int j = i + 1; j < n; ++j) {
                        if (row[j]) {
                            ans += cnt[{i, j}];
                            ++cnt[{i, j}];
                        }
                    }
                }
            }
        }
        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
func countCornerRectangles(grid [][]int) (ans int) {
    n := len(grid[0])
    type pair struct{ x, y int }
    cnt := map[pair]int{}
    for _, row := range grid {
        for i, x := range row {
            if x == 1 {
                for j := i + 1; j < n; j++ {
                    if row[j] == 1 {
                        t := pair{i, j}
                        ans += cnt[t]
                        cnt[t]++
                    }
                }
            }
        }
    }
    return
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
function countCornerRectangles(grid: number[][]): number {
    const n = grid[0].length;
    let ans = 0;
    const cnt: Map<number, number> = new Map();
    for (const row of grid) {
        for (let i = 0; i < n; ++i) {
            if (row[i] === 1) {
                for (let j = i + 1; j < n; ++j) {
                    if (row[j] === 1) {
                        const t = i * 200 + j;
                        ans += cnt.get(t) ?? 0;
                        cnt.set(t, (cnt.get(t) ?? 0) + 1);
                    }
                }
            }
        }
    }
    return ans;
}

Comments