Array
Breadth-First Search
Heap (Priority Queue)
Matrix
Description
You are asked to cut off all the trees in a forest for a golf event. The forest is represented as an m x n matrix. In this matrix:
0 means the cell cannot be walked through.1 represents an empty cell that can be walked through.A number greater than 1 represents a tree in a cell that can be walked through, and this number is the tree's height.
In one step, you can walk in any of the four directions: north, east, south, and west. If you are standing in a cell with a tree, you can choose whether to cut it off.
You must cut off the trees in order from shortest to tallest. When you cut off a tree, the value at its cell becomes 1 (an empty cell).
Starting from the point (0, 0), return the minimum steps you need to walk to cut off all the trees . If you cannot cut off all the trees, return -1.
Note: The input is generated such that no two trees have the same height, and there is at least one tree needs to be cut off.
Example 1:
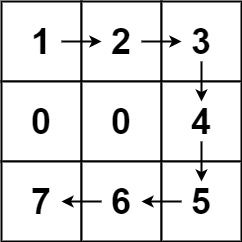
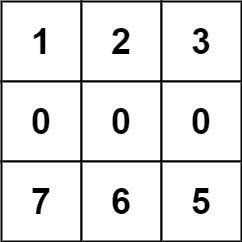
Input: forest = [[1,2,3],[0,0,4],[7,6,5]]
Output: 6
Explanation: Following the path above allows you to cut off the trees from shortest to tallest in 6 steps.
Example 2:
Input: forest = [[1,2,3],[0,0,0],[7,6,5]]
Output: -1
Explanation: The trees in the bottom row cannot be accessed as the middle row is blocked.
Example 3:
Input: forest = [[2,3,4],[0,0,5],[8,7,6]]
Output: 6
Explanation: You can follow the same path as Example 1 to cut off all the trees.
Note that you can cut off the first tree at (0, 0) before making any steps.
Constraints:
m == forest.lengthn == forest[i].length1 <= m, n <= 500 <= forest[i][j] <= 109 Heights of all trees are distinct .
Solutions
Solution 1
Python3 Java C++ Go Rust
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35 class Solution :
def cutOffTree ( self , forest : List [ List [ int ]]) -> int :
def f ( i , j , x , y ):
return abs ( i - x ) + abs ( j - y )
def bfs ( i , j , x , y ):
q = [( f ( i , j , x , y ), i , j )]
dist = { i * n + j : 0 }
while q :
_ , i , j = heappop ( q )
step = dist [ i * n + j ]
if ( i , j ) == ( x , y ):
return step
for a , b in [[ 0 , - 1 ], [ 0 , 1 ], [ - 1 , 0 ], [ 1 , 0 ]]:
c , d = i + a , j + b
if 0 <= c < m and 0 <= d < n and forest [ c ][ d ] > 0 :
if c * n + d not in dist or dist [ c * n + d ] > step + 1 :
dist [ c * n + d ] = step + 1
heappush ( q , ( dist [ c * n + d ] + f ( c , d , x , y ), c , d ))
return - 1
m , n = len ( forest ), len ( forest [ 0 ])
trees = [
( forest [ i ][ j ], i , j ) for i in range ( m ) for j in range ( n ) if forest [ i ][ j ] > 1
]
trees . sort ()
i = j = 0
ans = 0
for _ , x , y in trees :
t = bfs ( i , j , x , y )
if t == - 1 :
return - 1
ans += t
i , j = x , y
return ans
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66 class Solution {
private int [] dist = new int [ 3600 ] ;
private List < List < Integer >> forest ;
private int m ;
private int n ;
public int cutOffTree ( List < List < Integer >> forest ) {
this . forest = forest ;
m = forest . size ();
n = forest . get ( 0 ). size ();
List < int []> trees = new ArrayList <> ();
for ( int i = 0 ; i < m ; ++ i ) {
for ( int j = 0 ; j < n ; ++ j ) {
if ( forest . get ( i ). get ( j ) > 1 ) {
trees . add ( new int [] { forest . get ( i ). get ( j ), i * n + j });
}
}
}
trees . sort ( Comparator . comparingInt ( a -> a [ 0 ] ));
int ans = 0 ;
int start = 0 ;
for ( int [] tree : trees ) {
int end = tree [ 1 ] ;
int t = bfs ( start , end );
if ( t == - 1 ) {
return - 1 ;
}
ans += t ;
start = end ;
}
return ans ;
}
private int bfs ( int start , int end ) {
PriorityQueue < int []> q = new PriorityQueue <> ( Comparator . comparingInt ( a -> a [ 0 ] ));
q . offer ( new int [] { f ( start , end ), start });
Arrays . fill ( dist , Integer . MAX_VALUE );
dist [ start ] = 0 ;
int [] dirs = { - 1 , 0 , 1 , 0 , - 1 };
while ( ! q . isEmpty ()) {
int state = q . poll () [ 1 ] ;
if ( state == end ) {
return dist [ state ] ;
}
for ( int k = 0 ; k < 4 ; ++ k ) {
int x = state / n + dirs [ k ] ;
int y = state % n + dirs [ k + 1 ] ;
if ( x >= 0 && x < m && y >= 0 && y < n && forest . get ( x ). get ( y ) > 0 ) {
if ( dist [ x * n + y ] > dist [ state ] + 1 ) {
dist [ x * n + y ] = dist [ state ] + 1 ;
q . offer ( new int [] { dist [ x * n + y ] + f ( x * n + y , end ), x * n + y });
}
}
}
}
return - 1 ;
}
private int f ( int start , int end ) {
int a = start / n ;
int b = start % n ;
int c = end / n ;
int d = end % n ;
return Math . abs ( a - c ) + Math . abs ( b - d );
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55 class Solution {
public :
int m ;
int n ;
vector < int > dist ;
int cutOffTree ( vector < vector < int >>& forest ) {
m = forest . size ();
n = forest [ 0 ]. size ();
dist . resize ( 3600 );
vector < pair < int , int >> trees ;
for ( int i = 0 ; i < m ; ++ i )
for ( int j = 0 ; j < n ; ++ j )
if ( forest [ i ][ j ] > 1 )
trees . push_back ({ forest [ i ][ j ], i * n + j });
sort ( trees . begin (), trees . end ());
int ans = 0 ;
int start = 0 ;
for ( auto & tree : trees ) {
int end = tree . second ;
int t = bfs ( start , end , forest );
if ( t == -1 ) return -1 ;
ans += t ;
start = end ;
}
return ans ;
}
int bfs ( int start , int end , vector < vector < int >>& forest ) {
priority_queue < pair < int , int > , vector < pair < int , int >> , greater < pair < int , int >>> q ;
q . push ({ f ( start , end ), start });
fill ( dist . begin (), dist . end (), INT_MAX );
dist [ start ] = 0 ;
vector < int > dirs = { -1 , 0 , 1 , 0 , -1 };
while ( ! q . empty ()) {
int state = q . top (). second ;
q . pop ();
if ( state == end ) return dist [ state ];
for ( int k = 0 ; k < 4 ; ++ k ) {
int x = state / n + dirs [ k ], y = state % n + dirs [ k + 1 ];
if ( x >= 0 && x < m && y >= 0 && y < n && forest [ x ][ y ] && dist [ x * n + y ] > dist [ state ] + 1 ) {
dist [ x * n + y ] = dist [ state ] + 1 ;
q . push ({ dist [ x * n + y ] + f ( x * n + y , end ), x * n + y });
}
}
}
return -1 ;
}
int f ( int start , int end ) {
int a = start / n , b = start % n ;
int c = end / n , d = end % n ;
return abs ( a - c ) + abs ( b - d );
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60 var dirs = [][] int {{ - 1 , 0 }, { 1 , 0 }, { 0 , - 1 }, { 0 , 1 }}
type tree struct {
height int
pos int
}
func cutOffTree ( forest [][] int ) int {
row , col := len ( forest ), len ( forest [ 0 ])
bfs := func ( start , end int ) int {
q := [] int { start }
vis := make ( map [ int ] bool )
vis [ start ] = true
step := 0
for n := len ( q ); n > 0 ; n = len ( q ) {
for i := 0 ; i < n ; i ++ {
state := q [ 0 ]
q = q [ 1 :]
if state == end {
return step
}
for k := 0 ; k < 4 ; k ++ {
x , y := state / col + dirs [ k ][ 0 ], state % col + dirs [ k ][ 1 ]
nxt := x * col + y
if x >= 0 && x < row && y >= 0 && y < col && forest [ x ][ y ] != 0 && ! vis [ nxt ] {
q = append ( q , nxt )
vis [ nxt ] = true
}
}
}
step ++
}
return - 1
}
var trees [] tree
for i := 0 ; i < row ; i ++ {
for j := 0 ; j < col ; j ++ {
if forest [ i ][ j ] > 1 {
trees = append ( trees , tree { forest [ i ][ j ], i * col + j })
}
}
}
sort . Slice ( trees , func ( i , j int ) bool {
return trees [ i ]. height < trees [ j ]. height
})
ans , start := 0 , 0
for _ , t := range trees {
end := t . pos
step := bfs ( start , end )
if step == - 1 {
return - 1
}
ans += step
start = end
}
return ans
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67 use std :: collections :: HashSet ;
use std :: collections :: VecDeque ;
const DIRS : [[ i32 ; 2 ]; 4 ] = [[ - 1 , 0 ], [ 1 , 0 ], [ 0 , - 1 ], [ 0 , 1 ]];
impl Solution {
pub fn cut_off_tree ( forest : Vec < Vec < i32 >> ) -> i32 {
let ( row , col ) = ( forest . len () as i32 , forest [ 0 ]. len () as i32 );
let bfs = | start : i32 , end : i32 | -> i32 {
let mut queue = VecDeque :: new ();
let mut vis = HashSet :: new ();
queue . push_back ( start );
vis . insert ( start );
let mut step = 0 ;
while ! queue . is_empty () {
let n = queue . len ();
for _ in 0 .. n {
let state = queue . pop_front (). unwrap ();
if state == end {
return step ;
}
for k in 0 .. 4 {
let x = state / col + DIRS [ k ][ 0 ];
let y = ( state % col ) + DIRS [ k ][ 1 ];
let nxt = x * col + y ;
if x >= 0
&& x < row
&& y >= 0
&& y < col
&& forest [ x as usize ][ y as usize ] != 0
&& ! vis . contains ( & nxt )
{
queue . push_back ( nxt );
vis . insert ( nxt );
}
}
}
step += 1 ;
}
- 1
};
let mut trees = Vec :: new ();
for i in 0 .. row {
for j in 0 .. col {
let height = forest [ i as usize ][ j as usize ];
if height > 1 {
trees . push (( height , i * col + j ));
}
}
}
trees . sort ();
let ( mut ans , mut start ) = ( 0 , 0 );
for t in & trees {
let end = t . 1 ;
let step = bfs ( start , end );
if step == - 1 {
return - 1 ;
}
ans += step ;
start = end ;
}
ans
}
}
GitHub