563. Binary Tree Tilt

Description

Given the root of a binary tree, return the sum of every tree node's tilt.

The tilt of a tree node is the absolute difference between the sum of all left subtree node values and all right subtree node values. If a node does not have a left child, then the sum of the left subtree node values is treated as 0. The rule is similar if the node does not have a right child.

Example 1:

Input: root = [1,2,3]
Output: 1
Explanation: 
Tilt of node 2 : |0-0| = 0 (no children)
Tilt of node 3 : |0-0| = 0 (no children)
Tilt of node 1 : |2-3| = 1 (left subtree is just left child, so sum is 2; right subtree is just right child, so sum is 3)
Sum of every tilt : 0 + 0 + 1 = 1

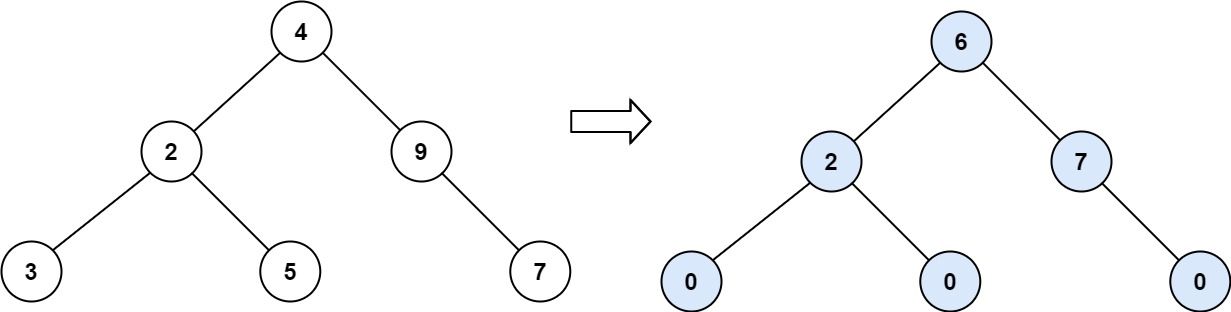
Example 2:

Input: root = [4,2,9,3,5,null,7]
Output: 15
Explanation: 
Tilt of node 3 : |0-0| = 0 (no children)
Tilt of node 5 : |0-0| = 0 (no children)
Tilt of node 7 : |0-0| = 0 (no children)
Tilt of node 2 : |3-5| = 2 (left subtree is just left child, so sum is 3; right subtree is just right child, so sum is 5)
Tilt of node 9 : |0-7| = 7 (no left child, so sum is 0; right subtree is just right child, so sum is 7)
Tilt of node 4 : |(3+5+2)-(9+7)| = |10-16| = 6 (left subtree values are 3, 5, and 2, which sums to 10; right subtree values are 9 and 7, which sums to 16)
Sum of every tilt : 0 + 0 + 0 + 2 + 7 + 6 = 15

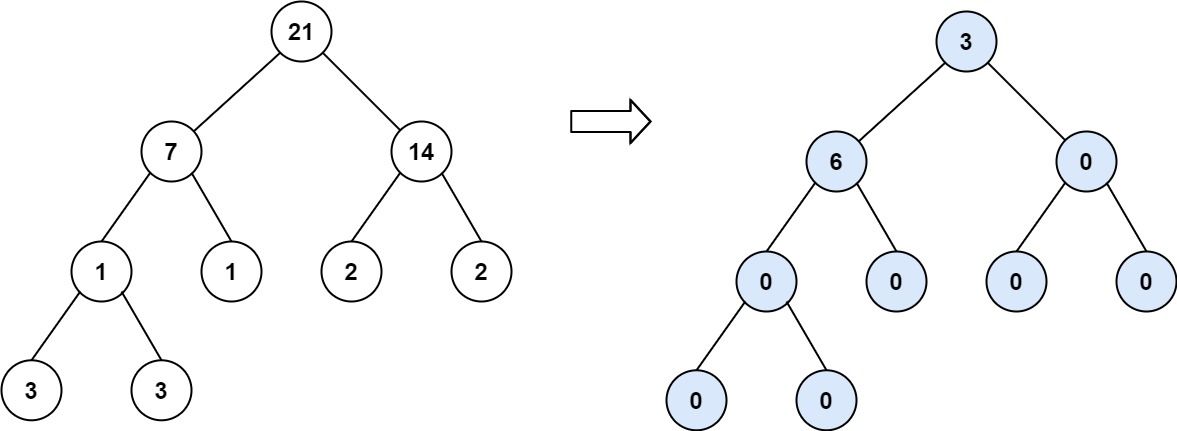
Example 3:

Input: root = [21,7,14,1,1,2,2,3,3]
Output: 9

Constraints:

The number of nodes in the tree is in the range [0, 10⁴].
-1000 <= Node.val <= 1000

Solutions

Solution 1: Recursion

We design a function \(\text{dfs}\) to calculate the sum of nodes in the subtree rooted at the current node. In the \(\text{dfs}\) function, we first check if the current node is null. If it is, we return 0. Then we recursively call the \(\text{dfs}\) function to calculate the sum of nodes in the left subtree \(l\) and the sum of nodes in the right subtree \(r\). Next, we calculate the tilt of the current node, which is \(|l - r|\), and add it to the answer. Finally, we return the sum of nodes of the current node, which is \(l + r + \textit{root.val}\).

In the main function, we initialize the answer to 0, then call the \(\text{dfs}\) function to calculate the tilt of the entire tree and return the answer.

The time complexity is \(O(n)\), and the space complexity is \(O(n)\), where \(n\) is the number of nodes.

Python3JavaC++GoTypeScript

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def findTilt(self, root: Optional[TreeNode]) -> int:
        def dfs(root: Optional[TreeNode]) -> int:
            if root is None:
                return 0
            l, r = dfs(root.left), dfs(root.right)
            nonlocal ans
            ans += abs(l - r)
            return l + r + root.val

        ans = 0
        dfs(root)
        return ans

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private int ans;

    public int findTilt(TreeNode root) {
        dfs(root);
        return ans;
    }

    private int dfs(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int l = dfs(root.left), r = dfs(root.right);
        ans += Math.abs(l - r);
        return l + r + root.val;
    }
}

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int findTilt(TreeNode* root) {
        int ans = 0;
        auto dfs = [&](this auto&& dfs, TreeNode* root) -> int {
            if (!root) {
                return 0;
            }
            int l = dfs(root->left), r = dfs(root->right);
            ans += abs(l - r);
            return l + r + root->val;
        };
        dfs(root);
        return ans;
    }
};

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func findTilt(root *TreeNode) (ans int) {
    var dfs func(*TreeNode) int
    dfs = func(root *TreeNode) int {
        if root == nil {
            return 0
        }
        l, r := dfs(root.Left), dfs(root.Right)
        ans += abs(l - r)
        return l + r + root.Val
    }
    dfs(root)
    return
}

func abs(x int) int {
    if x < 0 {
        return -x
    }
    return x
}

/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */

function findTilt(root: TreeNode | null): number {
    let ans: number = 0;
    const dfs = (root: TreeNode | null): number => {
        if (!root) {
            return 0;
        }
        const [l, r] = [dfs(root.left), dfs(root.right)];
        ans += Math.abs(l - r);
        return l + r + root.val;
    };
    dfs(root);
    return ans;
}

563. Binary Tree Tilt

Description

Solutions

Solution 1: Recursion

Comments