554. Brick Wall

Description

There is a rectangular brick wall in front of you with n rows of bricks. The ith row has some number of bricks each of the same height (i.e., one unit) but they can be of different widths. The total width of each row is the same.

Draw a vertical line from the top to the bottom and cross the least bricks. If your line goes through the edge of a brick, then the brick is not considered as crossed. You cannot draw a line just along one of the two vertical edges of the wall, in which case the line will obviously cross no bricks.

Given the 2D array wall that contains the information about the wall, return the minimum number of crossed bricks after drawing such a vertical line.

 

Example 1:

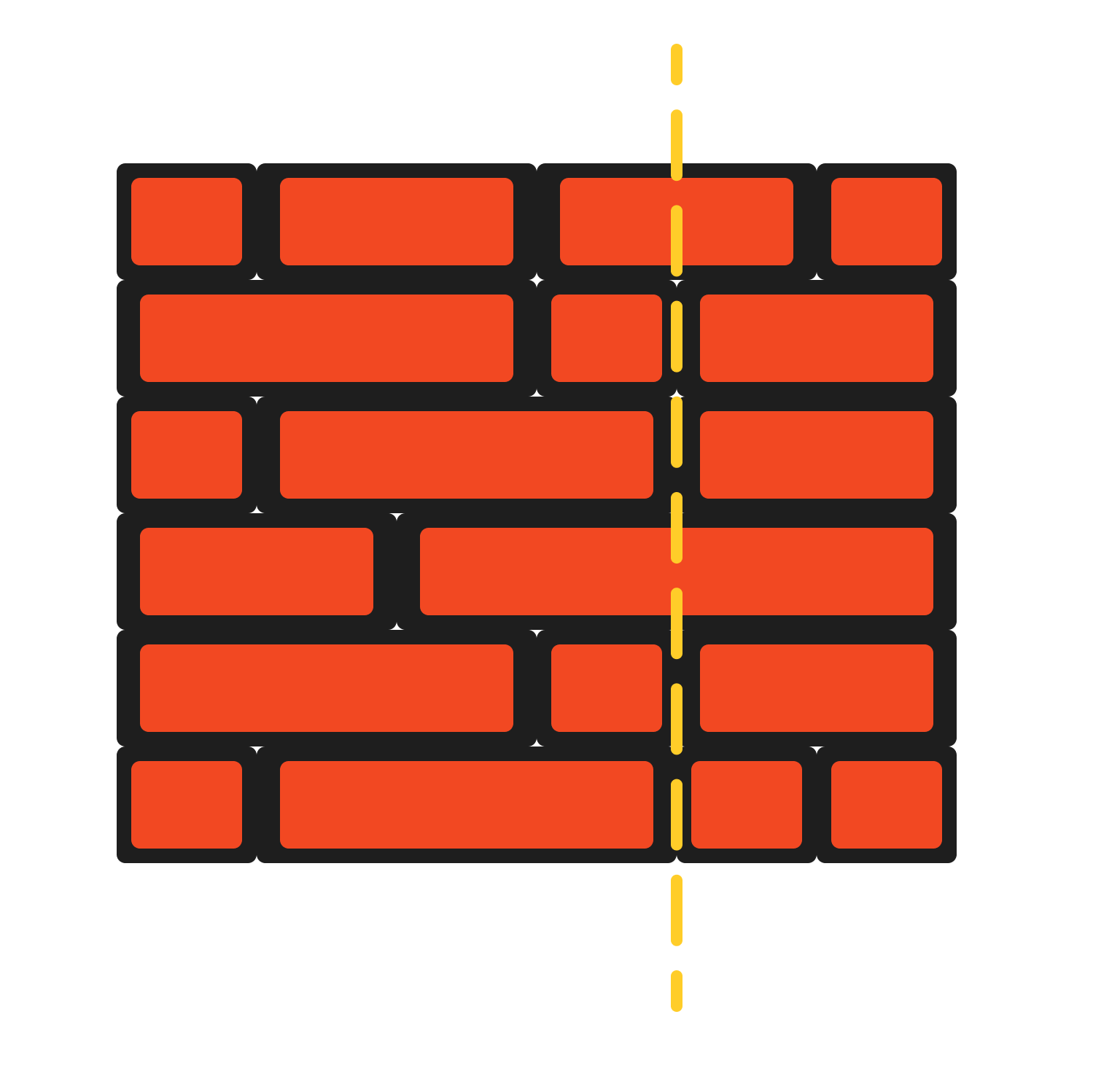
Input: wall = [[1,2,2,1],[3,1,2],[1,3,2],[2,4],[3,1,2],[1,3,1,1]]
Output: 2

Example 2:

Input: wall = [[1],[1],[1]]
Output: 3

 

Constraints:

• n == wall.length
• 1 <= n <= 104
• 1 <= wall[i].length <= 104
• 1 <= sum(wall[i].length) <= 2 * 104
• sum(wall[i]) is the same for each row i.
• 1 <= wall[i][j] <= 231 - 1

Solutions

Solution 1: Hash Table + Prefix Sum

We can use a hash table $\textit{cnt}$ to record the prefix sum of each row except for the last brick. The key is the value of the prefix sum, and the value is the number of times the prefix sum appears.

Traverse each row, and for each brick in the current row, add it to the current prefix sum and update $\textit{cnt}$.

Finally, we traverse $\textit{cnt}$ to find the prefix sum that appears the most times, which represents the situation where the least number of bricks are crossed. The final answer is the number of rows in the brick wall minus the number of bricks crossed.

The time complexity is $O(m \times n)$, and the space complexity is $O(n)$. Here, $m$ and $n$ are the number of rows and the number of bricks in the brick wall, respectively.

Python3JavaC++GoTypeScriptJavaScript

class Solution:
    def leastBricks(self, wall: List[List[int]]) -> int:
        cnt = Counter()
        for row in wall:
            s = 0
            for x in row[:-1]:
                s += x
                cnt[s] += 1
        return len(wall) - max(cnt.values(), default=0)

class Solution {
    public int leastBricks(List<List<Integer>> wall) {
        Map<Integer, Integer> cnt = new HashMap<>();
        for (var row : wall) {
            int s = 0;
            for (int i = 0; i + 1 < row.size(); ++i) {
                s += row.get(i);
                cnt.merge(s, 1, Integer::sum);
            }
        }
        int mx = 0;
        for (var x : cnt.values()) {
            mx = Math.max(mx, x);
        }
        return wall.size() - mx;
    }
}

class Solution {
public:
    int leastBricks(vector<vector<int>>& wall) {
        unordered_map<int, int> cnt;
        for (const auto& row : wall) {
            int s = 0;
            for (int i = 0; i + 1 < row.size(); ++i) {
                s += row[i];
                cnt[s]++;
            }
        }
        int mx = 0;
        for (const auto& [_, x] : cnt) {
            mx = max(mx, x);
        }
        return wall.size() - mx;
    }
};

func leastBricks(wall [][]int) int {
    cnt := map[int]int{}
    for _, row := range wall {
        s := 0
        for _, x := range row[:len(row)-1] {
            s += x
            cnt[s]++
        }
    }
    mx := 0
    for _, x := range cnt {
        mx = max(mx, x)
    }
    return len(wall) - mx
}

function leastBricks(wall: number[][]): number {
    const cnt: Map<number, number> = new Map();
    for (const row of wall) {
        let s = 0;
        for (let i = 0; i + 1 < row.length; ++i) {
            s += row[i];
            cnt.set(s, (cnt.get(s) || 0) + 1);
        }
    }
    const mx = Math.max(...cnt.values(), 0);
    return wall.length - mx;
}

/**
 * @param {number[][]} wall
 * @return {number}
 */
var leastBricks = function (wall) {
    const cnt = new Map();
    for (const row of wall) {
        let s = 0;
        for (let i = 0; i + 1 < row.length; ++i) {
            s += row[i];
            cnt.set(s, (cnt.get(s) || 0) + 1);
        }
    }
    const mx = Math.max(...cnt.values(), 0);
    return wall.length - mx;
};

Comments