Skip to content

54. Spiral Matrix

Description

Given an m x n matrix, return all elements of the matrix in spiral order.

 

Example 1:

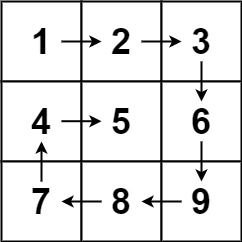
Input: matrix = [[1,2,3],[4,5,6],[7,8,9]]
Output: [1,2,3,6,9,8,7,4,5]

Example 2:

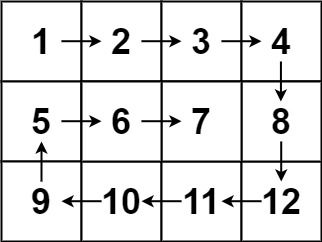
Input: matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
Output: [1,2,3,4,8,12,11,10,9,5,6,7]

 

Constraints:

  • m == matrix.length
  • n == matrix[i].length
  • 1 <= m, n <= 10
  • -100 <= matrix[i][j] <= 100

Solutions

Solution 1: Simulation

We use $i$ and $j$ to represent the row and column of the current element, use $k$ to represent the current direction, and use an array or hash table $vis$ to record whether each element has been visited. Each time we visit an element, we mark it as visited, then move forward in the current direction. If we find that it is out of bounds or has been visited after moving forward, we change the direction and continue to move forward until the entire matrix is traversed.

The time complexity is $O(m \times n)$, and the space complexity is $O(m \times n)$. Here, $m$ and $n$ are the number of rows and columns of the matrix, respectively.

For visited elements, we can also add a constant $300$ to their values, so we don't need an extra $vis$ array or hash table to record whether they have been visited, thereby reducing the space complexity to $O(1)$.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
class Solution:
    def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
        m, n = len(matrix), len(matrix[0])
        dirs = (0, 1, 0, -1, 0)
        i = j = k = 0
        ans = []
        vis = set()
        for _ in range(m * n):
            ans.append(matrix[i][j])
            vis.add((i, j))
            x, y = i + dirs[k], j + dirs[k + 1]
            if not 0 <= x < m or not 0 <= y < n or (x, y) in vis:
                k = (k + 1) % 4
            i = i + dirs[k]
            j = j + dirs[k + 1]
        return ans

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        int m = matrix.length, n = matrix[0].length;
        int[] dirs = {0, 1, 0, -1, 0};
        int i = 0, j = 0, k = 0;
        List<Integer> ans = new ArrayList<>();
        boolean[][] vis = new boolean[m][n];
        for (int h = m * n; h > 0; --h) {
            ans.add(matrix[i][j]);
            vis[i][j] = true;
            int x = i + dirs[k], y = j + dirs[k + 1];
            if (x < 0 || x >= m || y < 0 || y >= n || vis[x][y]) {
                k = (k + 1) % 4;
            }
            i += dirs[k];
            j += dirs[k + 1];
        }
        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    vector<int> spiralOrder(vector<vector<int>>& matrix) {
        int m = matrix.size(), n = matrix[0].size();
        int dirs[5] = {0, 1, 0, -1, 0};
        int i = 0, j = 0, k = 0;
        vector<int> ans;
        bool vis[m][n];
        memset(vis, false, sizeof(vis));
        for (int h = m * n; h; --h) {
            ans.push_back(matrix[i][j]);
            vis[i][j] = true;
            int x = i + dirs[k], y = j + dirs[k + 1];
            if (x < 0 || x >= m || y < 0 || y >= n || vis[x][y]) {
                k = (k + 1) % 4;
            }
            i += dirs[k];
            j += dirs[k + 1];
        }
        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
func spiralOrder(matrix [][]int) (ans []int) {
    m, n := len(matrix), len(matrix[0])
    vis := make([][]bool, m)
    for i := range vis {
        vis[i] = make([]bool, n)
    }
    dirs := [5]int{0, 1, 0, -1, 0}
    i, j, k := 0, 0, 0
    for h := m * n; h > 0; h-- {
        ans = append(ans, matrix[i][j])
        vis[i][j] = true
        x, y := i+dirs[k], j+dirs[k+1]
        if x < 0 || x >= m || y < 0 || y >= n || vis[x][y] {
            k = (k + 1) % 4
        }
        i, j = i+dirs[k], j+dirs[k+1]
    }
    return
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
function spiralOrder(matrix: number[][]): number[] {
    const m = matrix.length;
    const n = matrix[0].length;
    const ans: number[] = [];
    const vis = new Array(m).fill(0).map(() => new Array(n).fill(false));
    const dirs = [0, 1, 0, -1, 0];
    for (let h = m * n, i = 0, j = 0, k = 0; h > 0; --h) {
        ans.push(matrix[i][j]);
        vis[i][j] = true;
        const x = i + dirs[k];
        const y = j + dirs[k + 1];
        if (x < 0 || x >= m || y < 0 || y >= n || vis[x][y]) {
            k = (k + 1) % 4;
        }
        i += dirs[k];
        j += dirs[k + 1];
    }
    return ans;
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
impl Solution {
    pub fn spiral_order(matrix: Vec<Vec<i32>>) -> Vec<i32> {
        let mut x1 = 0;
        let mut y1 = 0;
        let mut x2 = matrix.len() - 1;
        let mut y2 = matrix[0].len() - 1;
        let mut result = vec![];

        while x1 <= x2 && y1 <= y2 {
            for j in y1..=y2 {
                result.push(matrix[x1][j]);
            }
            for i in x1 + 1..=x2 {
                result.push(matrix[i][y2]);
            }
            if x1 < x2 && y1 < y2 {
                for j in (y1..y2).rev() {
                    result.push(matrix[x2][j]);
                }
                for i in (x1 + 1..x2).rev() {
                    result.push(matrix[i][y1]);
                }
            }
            x1 += 1;
            y1 += 1;
            if x2 != 0 {
                x2 -= 1;
            }
            if y2 != 0 {
                y2 -= 1;
            }
        }
        return result;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
/**
 * @param {number[][]} matrix
 * @return {number[]}
 */
var spiralOrder = function (matrix) {
    const m = matrix.length;
    const n = matrix[0].length;
    const ans = [];
    const vis = new Array(m).fill(0).map(() => new Array(n).fill(false));
    const dirs = [0, 1, 0, -1, 0];
    for (let h = m * n, i = 0, j = 0, k = 0; h > 0; --h) {
        ans.push(matrix[i][j]);
        vis[i][j] = true;
        const x = i + dirs[k];
        const y = j + dirs[k + 1];
        if (x < 0 || x >= m || y < 0 || y >= n || vis[x][y]) {
            k = (k + 1) % 4;
        }
        i += dirs[k];
        j += dirs[k + 1];
    }
    return ans;
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
public class Solution {
    public IList<int> SpiralOrder(int[][] matrix) {
        int m = matrix.Length, n = matrix[0].Length;
        int[] dirs = new int[] {0, 1, 0, -1, 0};
        IList<int> ans = new List<int>();
        bool[,] visited = new bool[m, n];
        for (int h = m * n, i = 0, j = 0, k = 0; h > 0; --h) {
            ans.Add(matrix[i][j]);
            visited[i, j] = true;
            int x = i + dirs[k], y = j + dirs[k + 1];
            if (x < 0 || x >= m || y < 0 || y >= n || visited[x, y]) {
                k = (k + 1) % 4;
            }
            i += dirs[k];
            j += dirs[k + 1];
        }
        return ans;
    }
}

Solution 2: Layer-by-layer Simulation

We can also traverse and store the matrix elements from the outside to the inside, layer by layer.

The time complexity is $O(m \times n)$, and the space complexity is $O(1)$. Here, $m$ and $n$ are the number of rows and columns of the matrix, respectively.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
class Solution:
    def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
        m, n = len(matrix), len(matrix[0])
        dirs = (0, 1, 0, -1, 0)
        i = j = k = 0
        ans = []
        for _ in range(m * n):
            ans.append(matrix[i][j])
            matrix[i][j] += 300
            x, y = i + dirs[k], j + dirs[k + 1]
            if not 0 <= x < m or not 0 <= y < n or matrix[x][y] > 100:
                k = (k + 1) % 4
            i = i + dirs[k]
            j = j + dirs[k + 1]
        # for i in range(m):
        #     for j in range(n):
        #         matrix[i][j] -= 300
        return ans

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        int m = matrix.length, n = matrix[0].length;
        int[] dirs = {0, 1, 0, -1, 0};
        List<Integer> ans = new ArrayList<>();
        for (int h = m * n, i = 0, j = 0, k = 0; h > 0; --h) {
            ans.add(matrix[i][j]);
            matrix[i][j] += 300;
            int x = i + dirs[k], y = j + dirs[k + 1];
            if (x < 0 || x >= m || y < 0 || y >= n || matrix[x][y] > 100) {
                k = (k + 1) % 4;
            }
            i += dirs[k];
            j += dirs[k + 1];
        }
        // for (int i = 0; i < m; ++i) {
        //     for (int j = 0; j < n; ++j) {
        //         matrix[i][j] -= 300;
        //     }
        // }
        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    vector<int> spiralOrder(vector<vector<int>>& matrix) {
        int m = matrix.size(), n = matrix[0].size();
        int dirs[5] = {0, 1, 0, -1, 0};
        vector<int> ans;
        for (int h = m * n, i = 0, j = 0, k = 0; h; --h) {
            ans.push_back(matrix[i][j]);
            matrix[i][j] += 300;
            int x = i + dirs[k], y = j + dirs[k + 1];
            if (x < 0 || x >= m || y < 0 || y >= n || matrix[x][y] > 100) {
                k = (k + 1) % 4;
            }
            i += dirs[k];
            j += dirs[k + 1];
        }
        // for (int i = 0; i < m; ++i) {
        //     for (int j = 0; j < n; ++j) {
        //         matrix[i][j] -= 300;
        //     }
        // }
        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
func spiralOrder(matrix [][]int) (ans []int) {
    m, n := len(matrix), len(matrix[0])
    dirs := [5]int{0, 1, 0, -1, 0}
    for h, i, j, k := m*n, 0, 0, 0; h > 0; h-- {
        ans = append(ans, matrix[i][j])
        matrix[i][j] += 300
        x, y := i+dirs[k], j+dirs[k+1]
        if x < 0 || x >= m || y < 0 || y >= n || matrix[x][y] > 100 {
            k = (k + 1) % 4
        }
        i, j = i+dirs[k], j+dirs[k+1]
    }
    // for i, row := range matrix {
    //  for j := range row {
    //      matrix[i][j] -= 300
    //  }
    // }
    return
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
function spiralOrder(matrix: number[][]): number[] {
    const m = matrix.length;
    const n = matrix[0].length;
    const ans: number[] = [];
    const dirs = [0, 1, 0, -1, 0];
    for (let h = m * n, i = 0, j = 0, k = 0; h > 0; --h) {
        ans.push(matrix[i][j]);
        matrix[i][j] += 300;
        const x = i + dirs[k];
        const y = j + dirs[k + 1];
        if (x < 0 || x >= m || y < 0 || y >= n || matrix[x][y] > 100) {
            k = (k + 1) % 4;
        }
        i += dirs[k];
        j += dirs[k + 1];
    }
    // for (let i = 0; i < m; ++i) {
    //     for (let j = 0; j < n; ++j) {
    //         matrix[i][j] -= 300;
    //     }
    // }
    return ans;
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/**
 * @param {number[][]} matrix
 * @return {number[]}
 */
var spiralOrder = function (matrix) {
    const m = matrix.length;
    const n = matrix[0].length;
    const ans = [];
    const dirs = [0, 1, 0, -1, 0];
    for (let h = m * n, i = 0, j = 0, k = 0; h > 0; --h) {
        ans.push(matrix[i][j]);
        matrix[i][j] += 300;
        const x = i + dirs[k];
        const y = j + dirs[k + 1];
        if (x < 0 || x >= m || y < 0 || y >= n || matrix[x][y] > 100) {
            k = (k + 1) % 4;
        }
        i += dirs[k];
        j += dirs[k + 1];
    }
    // for (let i = 0; i < m; ++i) {
    //     for (let j = 0; j < n; ++j) {
    //         matrix[i][j] -= 300;
    //     }
    // }
    return ans;
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public class Solution {
    public IList<int> SpiralOrder(int[][] matrix) {
        int m = matrix.Length, n = matrix[0].Length;
        int[] dirs = new int[] {0, 1, 0, -1, 0};
        IList<int> ans = new List<int>();
        for (int h = m * n, i = 0, j = 0, k = 0; h > 0; --h) {
            ans.Add(matrix[i][j]);
            matrix[i][j] += 300;
            int x = i + dirs[k], y = j + dirs[k + 1];
            if (x < 0 || x >= m || y < 0 || y >= n || matrix[x][y] > 100) {
                k = (k + 1) % 4;
            }
            i += dirs[k];
            j += dirs[k + 1];
        }
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                matrix[i][j] -= 300;
            }
        }
        return ans;
    }
}

Solution 3

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
class Solution:
    def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
        m, n = len(matrix), len(matrix[0])
        x1, y1, x2, y2 = 0, 0, m - 1, n - 1
        ans = []
        while x1 <= x2 and y1 <= y2:
            for j in range(y1, y2 + 1):
                ans.append(matrix[x1][j])
            for i in range(x1 + 1, x2 + 1):
                ans.append(matrix[i][y2])
            if x1 < x2 and y1 < y2:
                for j in range(y2 - 1, y1 - 1, -1):
                    ans.append(matrix[x2][j])
                for i in range(x2 - 1, x1, -1):
                    ans.append(matrix[i][y1])
            x1, y1 = x1 + 1, y1 + 1
            x2, y2 = x2 - 1, y2 - 1
        return ans

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        int m = matrix.length, n = matrix[0].length;
        int x1 = 0, y1 = 0, x2 = m - 1, y2 = n - 1;
        List<Integer> ans = new ArrayList<>();
        while (x1 <= x2 && y1 <= y2) {
            for (int j = y1; j <= y2; ++j) {
                ans.add(matrix[x1][j]);
            }
            for (int i = x1 + 1; i <= x2; ++i) {
                ans.add(matrix[i][y2]);
            }
            if (x1 < x2 && y1 < y2) {
                for (int j = y2 - 1; j >= y1; --j) {
                    ans.add(matrix[x2][j]);
                }
                for (int i = x2 - 1; i > x1; --i) {
                    ans.add(matrix[i][y1]);
                }
            }
            ++x1;
            ++y1;
            --x2;
            --y2;
        }
        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    vector<int> spiralOrder(vector<vector<int>>& matrix) {
        int m = matrix.size(), n = matrix[0].size();
        int x1 = 0, y1 = 0, x2 = m - 1, y2 = n - 1;
        vector<int> ans;
        while (x1 <= x2 && y1 <= y2) {
            for (int j = y1; j <= y2; ++j) {
                ans.push_back(matrix[x1][j]);
            }
            for (int i = x1 + 1; i <= x2; ++i) {
                ans.push_back(matrix[i][y2]);
            }
            if (x1 < x2 && y1 < y2) {
                for (int j = y2 - 1; j >= y1; --j) {
                    ans.push_back(matrix[x2][j]);
                }
                for (int i = x2 - 1; i > x1; --i) {
                    ans.push_back(matrix[i][y1]);
                }
            }
            ++x1, ++y1;
            --x2, --y2;
        }
        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
func spiralOrder(matrix [][]int) (ans []int) {
    m, n := len(matrix), len(matrix[0])
    x1, y1, x2, y2 := 0, 0, m-1, n-1
    for x1 <= x2 && y1 <= y2 {
        for j := y1; j <= y2; j++ {
            ans = append(ans, matrix[x1][j])
        }
        for i := x1 + 1; i <= x2; i++ {
            ans = append(ans, matrix[i][y2])
        }
        if x1 < x2 && y1 < y2 {
            for j := y2 - 1; j >= y1; j-- {
                ans = append(ans, matrix[x2][j])
            }
            for i := x2 - 1; i > x1; i-- {
                ans = append(ans, matrix[i][y1])
            }
        }
        x1, y1 = x1+1, y1+1
        x2, y2 = x2-1, y2-1
    }
    return
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
function spiralOrder(matrix: number[][]): number[] {
    const m = matrix.length;
    const n = matrix[0].length;
    let x1 = 0;
    let y1 = 0;
    let x2 = m - 1;
    let y2 = n - 1;
    const ans: number[] = [];
    while (x1 <= x2 && y1 <= y2) {
        for (let j = y1; j <= y2; ++j) {
            ans.push(matrix[x1][j]);
        }
        for (let i = x1 + 1; i <= x2; ++i) {
            ans.push(matrix[i][y2]);
        }
        if (x1 < x2 && y1 < y2) {
            for (let j = y2 - 1; j >= y1; --j) {
                ans.push(matrix[x2][j]);
            }
            for (let i = x2 - 1; i > x1; --i) {
                ans.push(matrix[i][y1]);
            }
        }
        ++x1;
        ++y1;
        --x2;
        --y2;
    }
    return ans;
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
/**
 * @param {number[][]} matrix
 * @return {number[]}
 */
var spiralOrder = function (matrix) {
    const m = matrix.length;
    const n = matrix[0].length;
    let x1 = 0;
    let y1 = 0;
    let x2 = m - 1;
    let y2 = n - 1;
    const ans = [];
    while (x1 <= x2 && y1 <= y2) {
        for (let j = y1; j <= y2; ++j) {
            ans.push(matrix[x1][j]);
        }
        for (let i = x1 + 1; i <= x2; ++i) {
            ans.push(matrix[i][y2]);
        }
        if (x1 < x2 && y1 < y2) {
            for (let j = y2 - 1; j >= y1; --j) {
                ans.push(matrix[x2][j]);
            }
            for (let i = x2 - 1; i > x1; --i) {
                ans.push(matrix[i][y1]);
            }
        }
        ++x1;
        ++y1;
        --x2;
        --y2;
    }
    return ans;
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
public class Solution {
    public IList<int> SpiralOrder(int[][] matrix) {
        int m = matrix.Length, n = matrix[0].Length;
        int x1 = 0, y1 = 0, x2 = m - 1, y2 = n - 1;
        IList<int> ans = new List<int>();
        while (x1 <= x2 && y1 <= y2) {
            for (int j = y1; j <= y2; ++j) {
                ans.Add(matrix[x1][j]);
            }
            for (int i = x1 + 1; i <= x2; ++i) {
                ans.Add(matrix[i][y2]);
            }
            if (x1 < x2 && y1 < y2) {
                for (int j = y2 - 1; j >= y1; --j) {
                    ans.Add(matrix[x2][j]);
                }
                for (int i = x2 - 1; i > x1; --i) {
                    ans.Add(matrix[i][y1]);
                }
            }
            ++x1;
            ++y1;
            --x2;
            --y2;
        }
        return ans;
    }
}

Comments