Skip to content

422. Valid Word Square πŸ”’

Description

Given an array of strings words, return true if it forms a valid word square.

A sequence of strings forms a valid word square if the kth row and column read the same string, where 0 <= k < max(numRows, numColumns).

 

Example 1:

Input: words = ["abcd","bnrt","crmy","dtye"]
Output: true
Explanation:
The 1st row and 1st column both read "abcd".
The 2nd row and 2nd column both read "bnrt".
The 3rd row and 3rd column both read "crmy".
The 4th row and 4th column both read "dtye".
Therefore, it is a valid word square.

Example 2:

Input: words = ["abcd","bnrt","crm","dt"]
Output: true
Explanation:
The 1st row and 1st column both read "abcd".
The 2nd row and 2nd column both read "bnrt".
The 3rd row and 3rd column both read "crm".
The 4th row and 4th column both read "dt".
Therefore, it is a valid word square.

Example 3:

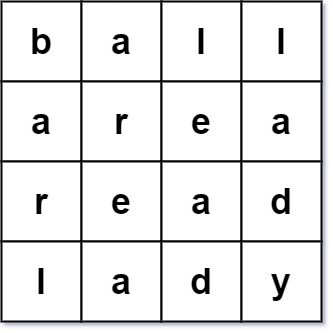
Input: words = ["ball","area","read","lady"]
Output: false
Explanation:
The 3rd row reads "read" while the 3rd column reads "lead".
Therefore, it is NOT a valid word square.

 

Constraints:

  • 1 <= words.length <= 500
  • 1 <= words[i].length <= 500
  • words[i] consists of only lowercase English letters.

Solutions

Solution 1: Iterative Check

We observe that if $words[i][j] \neq words[j][i]$, we can directly return false.

Therefore, we only need to iterate through each row, and then check whether each row satisfies $words[i][j] = words[j][i]$. Note that if the index is out of bounds, we also directly return false.

The time complexity is $O(n^2)$, where $n$ is the length of words. The space complexity is $O(1)`.

1
2
3
4
5
6
7
8
class Solution:
    def validWordSquare(self, words: List[str]) -> bool:
        m = len(words)
        for i, w in enumerate(words):
            for j, c in enumerate(w):
                if j >= m or i >= len(words[j]) or c != words[j][i]:
                    return False
        return True

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
class Solution {
    public boolean validWordSquare(List<String> words) {
        int m = words.size();
        for (int i = 0; i < m; ++i) {
            int n = words.get(i).length();
            for (int j = 0; j < n; ++j) {
                if (j >= m || i >= words.get(j).length()) {
                    return false;
                }
                if (words.get(i).charAt(j) != words.get(j).charAt(i)) {
                    return false;
                }
            }
        }
        return true;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
class Solution {
public:
    bool validWordSquare(vector<string>& words) {
        int m = words.size();
        for (int i = 0; i < m; ++i) {
            int n = words[i].size();
            for (int j = 0; j < n; ++j) {
                if (j >= m || i >= words[j].size() || words[i][j] != words[j][i]) {
                    return false;
                }
            }
        }
        return true;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
func validWordSquare(words []string) bool {
    m := len(words)
    for i, w := range words {
        for j := range w {
            if j >= m || i >= len(words[j]) || w[j] != words[j][i] {
                return false
            }
        }
    }
    return true
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
function validWordSquare(words: string[]): boolean {
    const m = words.length;
    for (let i = 0; i < m; ++i) {
        const n = words[i].length;
        for (let j = 0; j < n; ++j) {
            if (j >= m || i >= words[j].length || words[i][j] !== words[j][i]) {
                return false;
            }
        }
    }
    return true;
}

Comments