3425. Longest Special Path
Description
You are given an undirected tree rooted at node 0 with n nodes numbered from 0 to n - 1, represented by a 2D array edges of length n - 1, where edges[i] = [ui, vi, lengthi] indicates an edge between nodes ui and vi with length lengthi. You are also given an integer array nums, where nums[i] represents the value at node i.
A special path is defined as a downward path from an ancestor node to a descendant node such that all the values of the nodes in that path are unique.
Note that a path may start and end at the same node.
Return an array result of size 2, where result[0] is the length of the longest special path, and result[1] is the minimum number of nodes in all possible longest special paths.
Example 1:
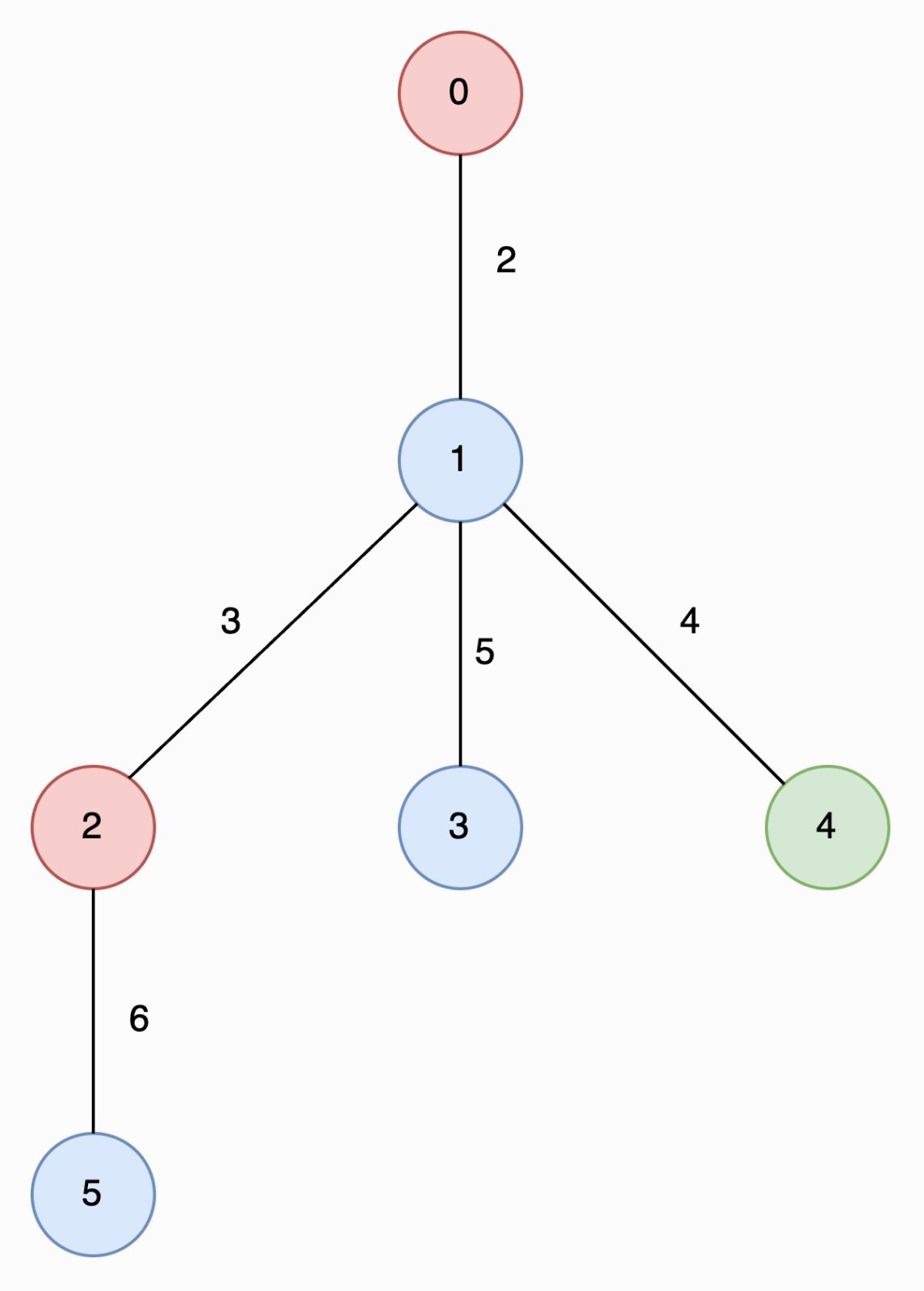
Input: edges = [[0,1,2],[1,2,3],[1,3,5],[1,4,4],[2,5,6]], nums = [2,1,2,1,3,1]
Output: [6,2]
Explanation:
In the image below, nodes are colored by their corresponding values in nums
The longest special paths are 2 -> 5 and 0 -> 1 -> 4, both having a length of 6. The minimum number of nodes across all longest special paths is 2.
Example 2:
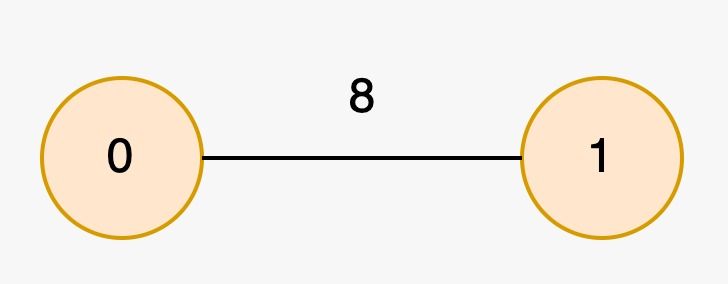
Input: edges = [[1,0,8]], nums = [2,2]
Output: [0,1]
Explanation:
The longest special paths are 0 and 1, both having a length of 0. The minimum number of nodes across all longest special paths is 1.
Constraints:
2 <= n <= 5 * 104edges.length == n - 1edges[i].length == 30 <= ui, vi < n1 <= lengthi <= 103nums.length == n0 <= nums[i] <= 5 * 104- The input is generated such that
edgesrepresents a valid tree.
Solutions
Solution 1
1 | |
1 | |
1 | |
1 | |