Skip to content

3382. Maximum Area Rectangle With Point Constraints II

Description

There are n points on an infinite plane. You are given two integer arrays xCoord and yCoord where (xCoord[i], yCoord[i]) represents the coordinates of the ith point.

Your task is to find the maximum area of a rectangle that:

  • Can be formed using four of these points as its corners.
  • Does not contain any other point inside or on its border.
  • Has its edges parallel to the axes.

Return the maximum area that you can obtain or -1 if no such rectangle is possible.

 

Example 1:

Input: xCoord = [1,1,3,3], yCoord = [1,3,1,3]

Output: 4

Explanation:

Example 1 diagram

We can make a rectangle with these 4 points as corners and there is no other point that lies inside or on the border. Hence, the maximum possible area would be 4.

Example 2:

Input: xCoord = [1,1,3,3,2], yCoord = [1,3,1,3,2]

Output: -1

Explanation:

Example 2 diagram

There is only one rectangle possible is with points [1,1], [1,3], [3,1] and [3,3] but [2,2] will always lie inside it. Hence, returning -1.

Example 3:

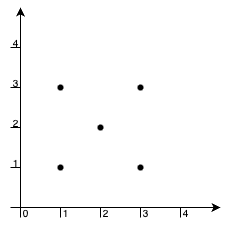
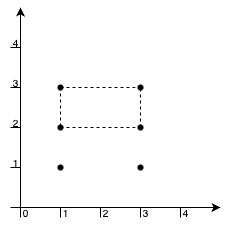
Input: xCoord = [1,1,3,3,1,3], yCoord = [1,3,1,3,2,2]

Output: 2

Explanation:

Example 3 diagram

The maximum area rectangle is formed by the points [1,3], [1,2], [3,2], [3,3], which has an area of 2. Additionally, the points [1,1], [1,2], [3,1], [3,2] also form a valid rectangle with the same area.

 

Constraints:

  • 1 <= xCoord.length == yCoord.length <= 2 * 105
  • 0 <= xCoord[i], yCoord[i] <= 8 * 107
  • All the given points are unique.

Solutions

Solution 1

1


1


1


1

Comments