3378. Count Connected Components in LCM Graph

Description

You are given an array of integers nums of size n and a positive integer threshold.

There is a graph consisting of n nodes with the i^th node having a value of nums[i]. Two nodes i and j in the graph are connected via an undirected edge if lcm(nums[i], nums[j]) <= threshold.

Return the number of connected components in this graph.

A connected component is a subgraph of a graph in which there exists a path between any two vertices, and no vertex of the subgraph shares an edge with a vertex outside of the subgraph.

The term lcm(a, b) denotes the least common multiple of a and b.

Example 1:

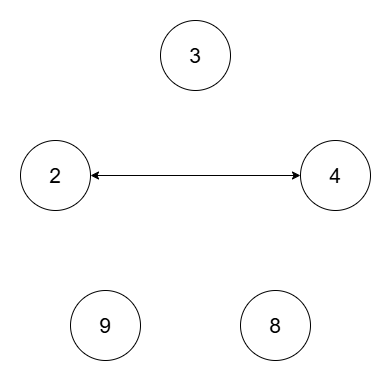
Input: nums = [2,4,8,3,9], threshold = 5

Output: 4

Explanation:

The four connected components are (2, 4), (3), (8), (9).

Example 2:

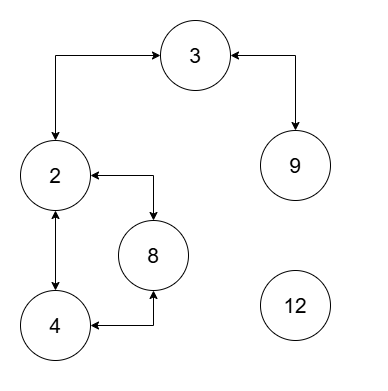
Input: nums = [2,4,8,3,9,12], threshold = 10

Output: 2

Explanation:

The two connected components are (2, 3, 4, 8, 9), and (12).

Constraints:

1 <= nums.length <= 10⁵
1 <= nums[i] <= 10⁹
All elements of nums are unique.
1 <= threshold <= 2 * 10⁵

Solutions

Solution 1: Union Find

Python3JavaC++Go

class DSU:
    def __init__(self, n):
        self.parent = {i: i for i in range(n)}
        self.rank = {i: 0 for i in range(n)}

    def make_set(self, v):
        self.parent[v] = v
        self.rank[v] = 1

    def find(self, x):
        if self.parent[x] != x:
            self.parent[x] = self.find(self.parent[x])
        return self.parent[x]

    def union_set(self, u, v):
        u = self.find(u)
        v = self.find(v)
        if u != v:
            if self.rank[u] < self.rank[v]:
                u, v = v, u
            self.parent[v] = u
            if self.rank[u] == self.rank[v]:
                self.rank[u] += 1


class Solution:
    def countComponents(self, nums, threshold):
        dsu = DSU(threshold + 1)

        for num in nums:
            for j in range(num, threshold + 1, num):
                dsu.union_set(num, j)

        unique_parents = set()
        for num in nums:
            if num > threshold:
                unique_parents.add(num)
            else:
                unique_parents.add(dsu.find(num))

        return len(unique_parents)

class DSU {
    private Map<Integer, Integer> parent;
    private Map<Integer, Integer> rank;

    public DSU(int n) {
        parent = new HashMap<>();
        rank = new HashMap<>();
        for (int i = 0; i <= n; i++) {
            parent.put(i, i);
            rank.put(i, 0);
        }
    }

    public void makeSet(int v) {
        parent.put(v, v);
        rank.put(v, 1);
    }

    public int find(int x) {
        if (parent.get(x) != x) {
            parent.put(x, find(parent.get(x)));
        }
        return parent.get(x);
    }

    public void unionSet(int u, int v) {
        u = find(u);
        v = find(v);
        if (u != v) {
            if (rank.get(u) < rank.get(v)) {
                int temp = u;
                u = v;
                v = temp;
            }
            parent.put(v, u);
            if (rank.get(u).equals(rank.get(v))) {
                rank.put(u, rank.get(u) + 1);
            }
        }
    }
}

class Solution {
    public int countComponents(int[] nums, int threshold) {
        DSU dsu = new DSU(threshold);

        for (int num : nums) {
            for (int j = num; j <= threshold; j += num) {
                dsu.unionSet(num, j);
            }
        }

        Set<Integer> uniqueParents = new HashSet<>();
        for (int num : nums) {
            if (num > threshold) {
                uniqueParents.add(num);
            } else {
                uniqueParents.add(dsu.find(num));
            }
        }

        return uniqueParents.size();
    }
}

typedef struct DSU {
    unordered_map<int, int> par, rank;
    DSU(int n) {
        for (int i = 0; i < n; ++i) {
            par[i] = i;
            rank[i] = 0;
        }
    }

    void makeSet(int v) {
        par[v] = v;
        rank[v] = 1;
    }

    int find(int x) {
        if (par[x] == x) {
            return x;
        }
        return par[x] = find(par[x]);
    }

    void unionSet(int u, int v) {
        u = find(u);
        v = find(v);
        if (u != v) {
            if (rank[u] < rank[v]) swap(u, v);
            par[v] = u;
            if (rank[u] == rank[v]) rank[u]++;
        }
    }
} DSU;

class Solution {
public:
    int countComponents(vector<int> &nums, int threshold) {
        DSU dsu(threshold);
        for (auto &num : nums) {
            for (int j = num; j <= threshold; j += num) {
                dsu.unionSet(num, j);
            }
        }
        unordered_set<int> par;
        for (auto &num : nums) {
            if (num > threshold) {
                par.insert(num);
            } else {
                par.insert(dsu.find(num));
            }
        }
        return par.size();
    }
};

type DSU struct {
    parent map[int]int
    rank   map[int]int
}

func NewDSU(n int) *DSU {
    dsu := &DSU{
        parent: make(map[int]int),
        rank:   make(map[int]int),
    }
    for i := 0; i <= n; i++ {
        dsu.parent[i] = i
        dsu.rank[i] = 0
    }
    return dsu
}

func (dsu *DSU) Find(x int) int {
    if dsu.parent[x] != x {
        dsu.parent[x] = dsu.Find(dsu.parent[x])
    }
    return dsu.parent[x]
}

func (dsu *DSU) Union(u, v int) {
    uRoot := dsu.Find(u)
    vRoot := dsu.Find(v)
    if uRoot != vRoot {
        if dsu.rank[uRoot] < dsu.rank[vRoot] {
            uRoot, vRoot = vRoot, uRoot
        }
        dsu.parent[vRoot] = uRoot
        if dsu.rank[uRoot] == dsu.rank[vRoot] {
            dsu.rank[uRoot]++
        }
    }
}

func countComponents(nums []int, threshold int) int {
    dsu := NewDSU(threshold)

    for _, num := range nums {
        for j := num; j <= threshold; j += num {
            dsu.Union(num, j)
        }
    }

    uniqueParents := make(map[int]struct{})
    for _, num := range nums {
        if num > threshold {
            uniqueParents[num] = struct{}{}
        } else {
            uniqueParents[dsu.Find(num)] = struct{}{}
        }
    }

    return len(uniqueParents)
}

Solution 2: DFS