3367. Maximize Sum of Weights after Edge Removals

Description

There exists an undirected tree with n nodes numbered 0 to n - 1. You are given a 2D integer array edges of length n - 1, where edges[i] = [ui, vi, wi] indicates that there is an edge between nodes ui and vi with weight wi in the tree.

Your task is to remove zero or more edges such that:

• Each node has an edge with at most k other nodes, where k is given.
• The sum of the weights of the remaining edges is maximized.

Return the maximum possible sum of weights for the remaining edges after making the necessary removals.

 

Example 1:

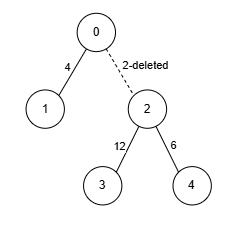
Input: edges = [[0,1,4],[0,2,2],[2,3,12],[2,4,6]], k = 2

Output: 22

Explanation:

• Node 2 has edges with 3 other nodes. We remove the edge [0, 2, 2], ensuring that no node has edges with more than k = 2 nodes.
• The sum of weights is 22, and we can't achieve a greater sum. Thus, the answer is 22.

Example 2:

Input: edges = [[0,1,5],[1,2,10],[0,3,15],[3,4,20],[3,5,5],[0,6,10]], k = 3

Output: 65

Explanation:

• Since no node has edges connecting it to more than k = 3 nodes, we don't remove any edges.
• The sum of weights is 65. Thus, the answer is 65.

 

Constraints:

• 2 <= n <= 105
• 1 <= k <= n - 1
• edges.length == n - 1
• edges[i].length == 3
• 0 <= edges[i][0] <= n - 1
• 0 <= edges[i][1] <= n - 1
• 1 <= edges[i][2] <= 106
• The input is generated such that edges form a valid tree.

Solutions

Solution 1

Python3JavaC++GoTypeScript

class Solution:
    def maximizeSumOfWeights(self, edges: List[List[int]], k: int) -> int:
        def dfs(u: int, fa: int) -> Tuple[int, int]:
            s = 0
            t = []
            for v, w in g[u]:
                if v == fa:
                    continue
                a, b = dfs(v, u)
                s += a
                if (d := (w + b - a)) > 0:
                    t.append(d)
            t.sort(reverse=True)
            return s + sum(t[:k]), s + sum(t[: k - 1])

        n = len(edges) + 1
        g: List[List[Tuple[int, int]]] = [[] for _ in range(n)]
        for u, v, w in edges:
            g[u].append((v, w))
            g[v].append((u, w))
        x, y = dfs(0, -1)
        return max(x, y)

class Solution {
    private List<int[]>[] g;
    private int k;

    public long maximizeSumOfWeights(int[][] edges, int k) {
        this.k = k;
        int n = edges.length + 1;
        g = new List[n];
        Arrays.setAll(g, i -> new ArrayList<>());
        for (var e : edges) {
            int u = e[0], v = e[1], w = e[2];
            g[u].add(new int[] {v, w});
            g[v].add(new int[] {u, w});
        }
        var ans = dfs(0, -1);
        return Math.max(ans[0], ans[1]);
    }

    private long[] dfs(int u, int fa) {
        long s = 0;
        List<Long> t = new ArrayList<>();
        for (var e : g[u]) {
            int v = e[0], w = e[1];
            if (v == fa) {
                continue;
            }
            var res = dfs(v, u);
            s += res[0];
            long d = w + res[1] - res[0];
            if (d > 0) {
                t.add(d);
            }
        }
        t.sort(Comparator.reverseOrder());
        for (int i = 0; i < Math.min(t.size(), k - 1); ++i) {
            s += t.get(i);
        }
        return new long[] {s + (t.size() >= k ? t.get(k - 1) : 0), s};
    }
}

class Solution {
public:
    long long maximizeSumOfWeights(vector<vector<int>>& edges, int k) {
        int n = edges.size() + 1;
        vector<vector<pair<int, int>>> g(n);
        for (auto& e : edges) {
            int u = e[0], v = e[1], w = e[2];
            g[u].emplace_back(v, w);
            g[v].emplace_back(u, w);
        }
        using ll = long long;
        auto dfs = [&](auto&& dfs, int u, int fa) -> pair<ll, ll> {
            ll s = 0;
            vector<ll> t;
            for (auto& [v, w] : g[u]) {
                if (v == fa) {
                    continue;
                }
                auto [a, b] = dfs(dfs, v, u);
                s += a;
                ll d = w + b - a;
                if (d > 0) {
                    t.push_back(d);
                }
            }
            ranges::sort(t, greater<>());
            for (int i = 0; i < min((int) t.size(), k - 1); ++i) {
                s += t[i];
            }
            return {s + (t.size() >= k ? t[k - 1] : 0), s};
        };

        auto [x, y] = dfs(dfs, 0, -1);
        return max(x, y);
    }
};

func maximizeSumOfWeights(edges [][]int, k int) int64 {
    n := len(edges) + 1
    g := make([][][]int, n)
    for _, e := range edges {
        u, v, w := e[0], e[1], e[2]
        g[u] = append(g[u], []int{v, w})
        g[v] = append(g[v], []int{u, w})
    }

    var dfs func(u, fa int) (int64, int64)
    dfs = func(u, fa int) (int64, int64) {
        var s int64
        var t []int64
        for _, e := range g[u] {
            v, w := e[0], e[1]
            if v == fa {
                continue
            }
            a, b := dfs(v, u)
            s += a
            d := int64(w) + b - a
            if d > 0 {
                t = append(t, d)
            }
        }
        sort.Slice(t, func(i, j int) bool {
            return t[i] > t[j]
        })
        for i := 0; i < min(len(t), k-1); i++ {
            s += t[i]
        }
        s2 := s
        if len(t) >= k {
            s += t[k-1]
        }
        return s, s2
    }

    x, y := dfs(0, -1)
    return max(x, y)
}

function maximizeSumOfWeights(edges: number[][], k: number): number {
    const n = edges.length + 1;
    const g: [number, number][][] = Array.from({ length: n }, () => []);
    for (const [u, v, w] of edges) {
        g[u].push([v, w]);
        g[v].push([u, w]);
    }
    const dfs = (u: number, fa: number): [number, number] => {
        let s = 0;
        const t: number[] = [];

        for (const [v, w] of g[u]) {
            if (v === fa) continue;

            const [a, b] = dfs(v, u);
            s += a;
            const d = w + b - a;
            if (d > 0) t.push(d);
        }

        t.sort((a, b) => b - a);
        for (let i = 0; i < Math.min(t.length, k - 1); i++) {
            s += t[i];
        }
        const s2 = s;
        if (t.length >= k) {
            s += t[k - 1];
        }

        return [s, s2];
    };

    const [x, y] = dfs(0, -1);
    return Math.max(x, y);
}

Comments