3249. Count the Number of Good Nodes

Description

There is an undirected tree with n nodes labeled from 0 to n - 1, and rooted at node 0. You are given a 2D integer array edges of length n - 1, where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree.

A node is good if all the subtrees rooted at its children have the same size.

Return the number of good nodes in the given tree.

A subtree of treeName is a tree consisting of a node in treeName and all of its descendants.

 

Example 1:

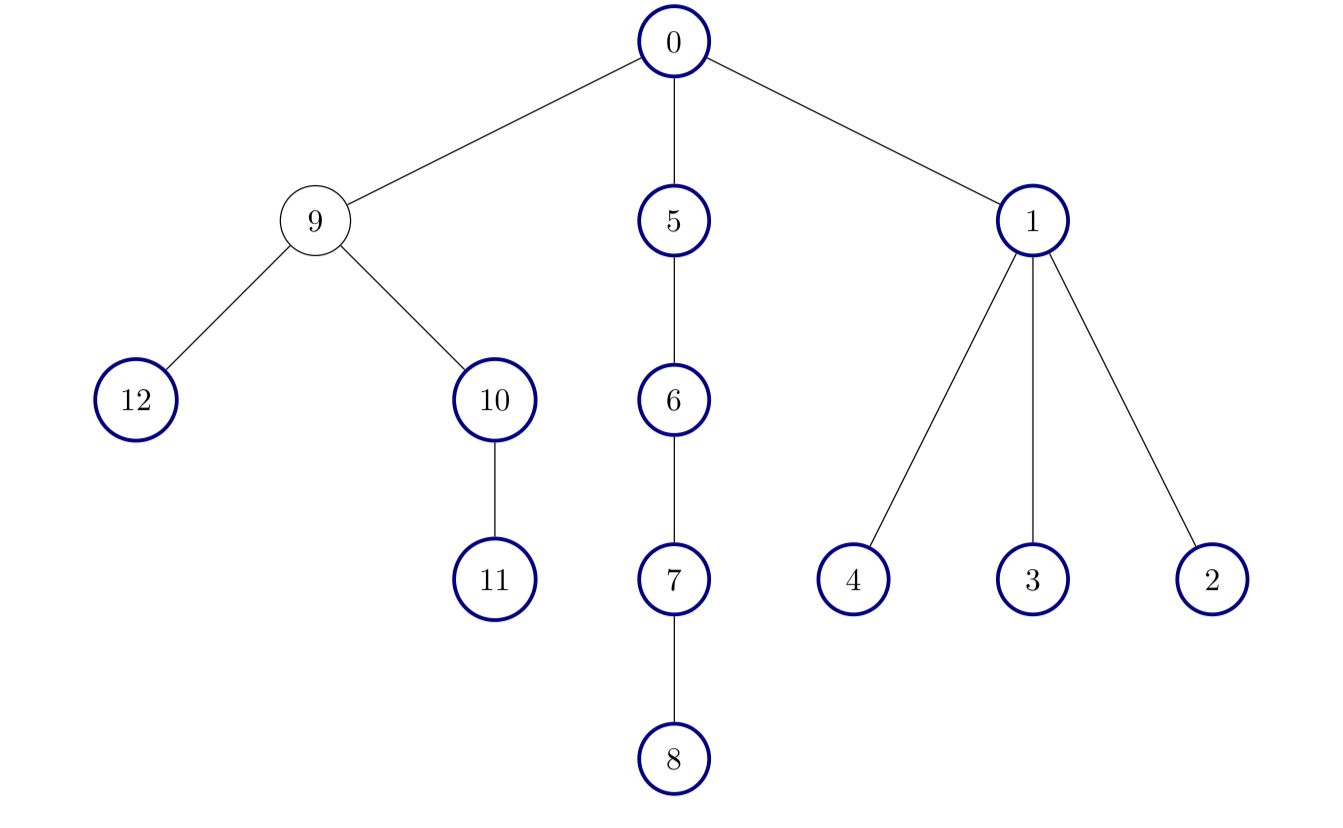
Input: edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]]

Output: 7

Explanation:

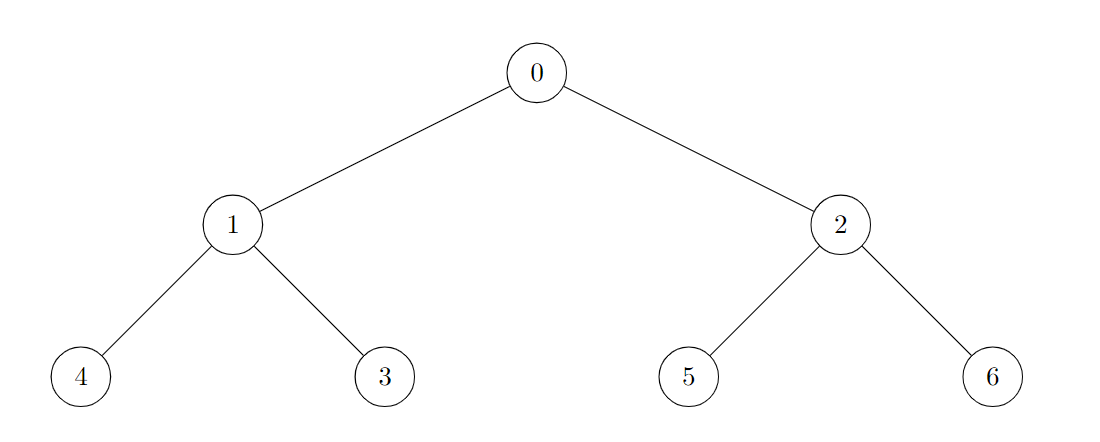
All of the nodes of the given tree are good.

Example 2:

Input: edges = [[0,1],[1,2],[2,3],[3,4],[0,5],[1,6],[2,7],[3,8]]

Output: 6

Explanation:

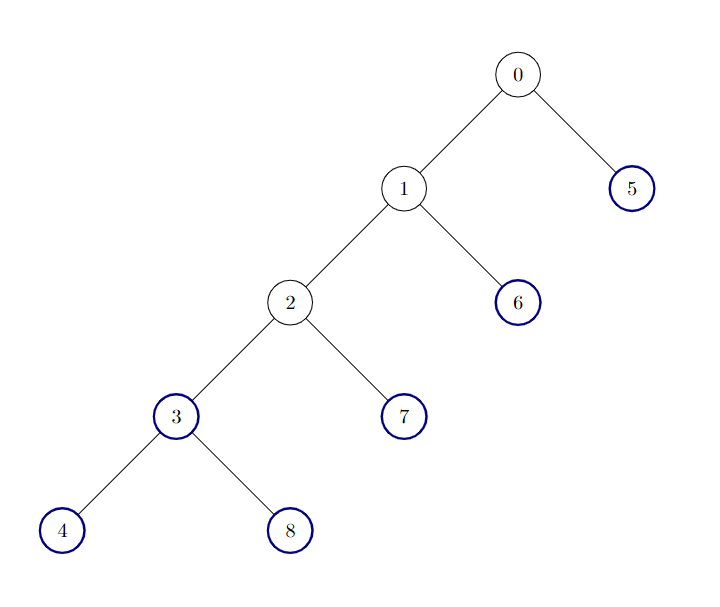
There are 6 good nodes in the given tree. They are colored in the image above.

Example 3:

Input: edges = [[0,1],[1,2],[1,3],[1,4],[0,5],[5,6],[6,7],[7,8],[0,9],[9,10],[9,12],[10,11]]

Output: 12

Explanation:

All nodes except node 9 are good.

 

Constraints:

• 2 <= n <= 105
• edges.length == n - 1
• edges[i].length == 2
• 0 <= ai, bi < n
• The input is generated such that edges represents a valid tree.

Solutions

Solution 1: DFS

First, we construct the adjacency list \(\textit{g}\) of the tree based on the given edges \(\textit{edges}\), where \(\textit{g}[a]\) represents all the neighboring nodes of node \(a\).

Next, we design a function \(\textit{dfs}(a, \textit{fa})\) to calculate the number of nodes in the subtree rooted at node \(a\) and to accumulate the count of good nodes. Here, \(\textit{fa}\) represents the parent node of node \(a\).

The execution process of the function \(\textit{dfs}(a, \textit{fa})\) is as follows:

1. Initialize variables \(\textit{pre} = -1\), \(\textit{cnt} = 1\), \(\textit{ok} = 1\), representing the number of nodes in a subtree of node \(a\), the total number of nodes in all subtrees of node \(a\), and whether node \(a\) is a good node, respectively.
2. Traverse all neighboring nodes \(b\) of node \(a\). If \(b\) is not equal to \(\textit{fa}\), recursively call \(\textit{dfs}(b, a)\), with the return value being \(\textit{cur}\), and add \(\textit{cur}\) to \(\textit{cnt}\). If \(\textit{pre} < 0\), assign \(\textit{cur}\) to \(\textit{pre}\); otherwise, if \(\textit{pre}\) is not equal to \(\textit{cur}\), it means the number of nodes in different subtrees of node \(a\) is different, and set \(\textit{ok}\) to \(0\).
3. Finally, add \(\textit{ok}\) to the answer and return \(\textit{cnt}\).

In the main function, we call \(\textit{dfs}(0, -1)\) and return the final answer.

The time complexity is \(O(n)\), and the space complexity is \(O(n)\). Here, \(n\) represents the number of nodes.

Python3JavaC++GoTypeScript

class Solution:
    def countGoodNodes(self, edges: List[List[int]]) -> int:
        def dfs(a: int, fa: int) -> int:
            pre = -1
            cnt = ok = 1
            for b in g[a]:
                if b != fa:
                    cur = dfs(b, a)
                    cnt += cur
                    if pre < 0:
                        pre = cur
                    elif pre != cur:
                        ok = 0
            nonlocal ans
            ans += ok
            return cnt

        g = defaultdict(list)
        for a, b in edges:
            g[a].append(b)
            g[b].append(a)
        ans = 0
        dfs(0, -1)
        return ans

class Solution {
    private int ans;
    private List<Integer>[] g;

    public int countGoodNodes(int[][] edges) {
        int n = edges.length + 1;
        g = new List[n];
        Arrays.setAll(g, k -> new ArrayList<>());
        for (var e : edges) {
            int a = e[0], b = e[1];
            g[a].add(b);
            g[b].add(a);
        }
        dfs(0, -1);
        return ans;
    }

    private int dfs(int a, int fa) {
        int pre = -1, cnt = 1, ok = 1;
        for (int b : g[a]) {
            if (b != fa) {
                int cur = dfs(b, a);
                cnt += cur;
                if (pre < 0) {
                    pre = cur;
                } else if (pre != cur) {
                    ok = 0;
                }
            }
        }
        ans += ok;
        return cnt;
    }
}

class Solution {
public:
    int countGoodNodes(vector<vector<int>>& edges) {
        int n = edges.size() + 1;
        vector<int> g[n];
        for (const auto& e : edges) {
            int a = e[0], b = e[1];
            g[a].push_back(b);
            g[b].push_back(a);
        }
        int ans = 0;
        auto dfs = [&](this auto&& dfs, int a, int fa) -> int {
            int pre = -1, cnt = 1, ok = 1;
            for (int b : g[a]) {
                if (b != fa) {
                    int cur = dfs(b, a);
                    cnt += cur;
                    if (pre < 0) {
                        pre = cur;
                    } else if (pre != cur) {
                        ok = 0;
                    }
                }
            }
            ans += ok;
            return cnt;
        };
        dfs(0, -1);
        return ans;
    }
};

func countGoodNodes(edges [][]int) (ans int) {
    n := len(edges) + 1
    g := make([][]int, n)
    for _, e := range edges {
        a, b := e[0], e[1]
        g[a] = append(g[a], b)
        g[b] = append(g[b], a)
    }
    var dfs func(int, int) int
    dfs = func(a, fa int) int {
        pre, cnt, ok := -1, 1, 1
        for _, b := range g[a] {
            if b != fa {
                cur := dfs(b, a)
                cnt += cur
                if pre < 0 {
                    pre = cur
                } else if pre != cur {
                    ok = 0
                }
            }
        }
        ans += ok
        return cnt
    }
    dfs(0, -1)
    return
}

function countGoodNodes(edges: number[][]): number {
    const n = edges.length + 1;
    const g: number[][] = Array.from({ length: n }, () => []);
    for (const [a, b] of edges) {
        g[a].push(b);
        g[b].push(a);
    }
    let ans = 0;
    const dfs = (a: number, fa: number): number => {
        let [pre, cnt, ok] = [-1, 1, 1];
        for (const b of g[a]) {
            if (b !== fa) {
                const cur = dfs(b, a);
                cnt += cur;
                if (pre < 0) {
                    pre = cur;
                } else if (pre !== cur) {
                    ok = 0;
                }
            }
        }
        ans += ok;
        return cnt;
    };
    dfs(0, -1);
    return ans;
}

Comments