Skip to content

3244. Shortest Distance After Road Addition Queries II

Description

You are given an integer n and a 2D integer array queries.

There are n cities numbered from 0 to n - 1. Initially, there is a unidirectional road from city i to city i + 1 for all 0 <= i < n - 1.

queries[i] = [ui, vi] represents the addition of a new unidirectional road from city ui to city vi. After each query, you need to find the length of the shortest path from city 0 to city n - 1.

There are no two queries such that queries[i][0] < queries[j][0] < queries[i][1] < queries[j][1].

Return an array answer where for each i in the range [0, queries.length - 1], answer[i] is the length of the shortest path from city 0 to city n - 1 after processing the first i + 1 queries.

 

Example 1:

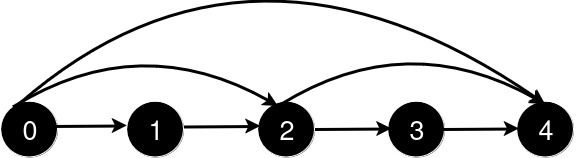
Input: n = 5, queries = [[2,4],[0,2],[0,4]]

Output: [3,2,1]

Explanation:

After the addition of the road from 2 to 4, the length of the shortest path from 0 to 4 is 3.

After the addition of the road from 0 to 2, the length of the shortest path from 0 to 4 is 2.

After the addition of the road from 0 to 4, the length of the shortest path from 0 to 4 is 1.

Example 2:

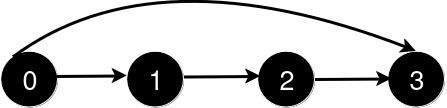
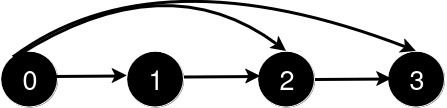
Input: n = 4, queries = [[0,3],[0,2]]

Output: [1,1]

Explanation:

After the addition of the road from 0 to 3, the length of the shortest path from 0 to 3 is 1.

After the addition of the road from 0 to 2, the length of the shortest path remains 1.

 

Constraints:

  • 3 <= n <= 105
  • 1 <= queries.length <= 105
  • queries[i].length == 2
  • 0 <= queries[i][0] < queries[i][1] < n
  • 1 < queries[i][1] - queries[i][0]
  • There are no repeated roads among the queries.
  • There are no two queries such that i != j and queries[i][0] < queries[j][0] < queries[i][1] < queries[j][1].

Solutions

Solution 1: Greedy + Recording Jump Positions

We define an array $\textit{nxt}$ of length $n - 1$, where $\textit{nxt}[i]$ represents the next city that can be reached from city $i$. Initially, $\textit{nxt}[i] = i + 1$.

For each query $[u, v]$, if $u'$ and $v'$ have already been connected before, and $u' \leq u < v \leq v'$, then we can skip this query. Otherwise, we need to set the next city number for cities from $\textit{nxt}[u]$ to $\textit{nxt}[v - 1]$ to $0$, and set $\textit{nxt}[u]$ to $v$.

During this process, we maintain a variable $\textit{cnt}$, which represents the length of the shortest path from city $0$ to city $n - 1$. Initially, $\textit{cnt} = n - 1$. Each time we set the next city number for cities in $[\textit{nxt}[u], \textit{v})$ to $0$, $\textit{cnt}$ decreases by $1$.

Time complexity is $O(n + q)$, and space complexity is $O(n)$. Here, $n$ and $q$ are the number of cities and the number of queries, respectively.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
class Solution:
    def shortestDistanceAfterQueries(
        self, n: int, queries: List[List[int]]
    ) -> List[int]:
        nxt = list(range(1, n))
        ans = []
        cnt = n - 1
        for u, v in queries:
            if 0 < nxt[u] < v:
                i = nxt[u]
                while i < v:
                    cnt -= 1
                    nxt[i], i = 0, nxt[i]
                nxt[u] = v
            ans.append(cnt)
        return ans

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    public int[] shortestDistanceAfterQueries(int n, int[][] queries) {
        int[] nxt = new int[n - 1];
        for (int i = 1; i < n; ++i) {
            nxt[i - 1] = i;
        }
        int m = queries.length;
        int cnt = n - 1;
        int[] ans = new int[m];
        for (int i = 0; i < m; ++i) {
            int u = queries[i][0], v = queries[i][1];
            if (nxt[u] > 0 && nxt[u] < v) {
                int j = nxt[u];
                while (j < v) {
                    --cnt;
                    int t = nxt[j];
                    nxt[j] = 0;
                    j = t;
                }
                nxt[u] = v;
            }
            ans[i] = cnt;
        }
        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    vector<int> shortestDistanceAfterQueries(int n, vector<vector<int>>& queries) {
        vector<int> nxt(n - 1);
        iota(nxt.begin(), nxt.end(), 1);
        int cnt = n - 1;
        vector<int> ans;
        for