Breadth-First Search
Depth-First Search
Graph
Union Find
Description
You have a graph of n nodes. You are given an integer n and an array edges where edges[i] = [ai , bi ] indicates that there is an edge between ai and bi in the graph.
Return the number of connected components in the graph .
Example 1:
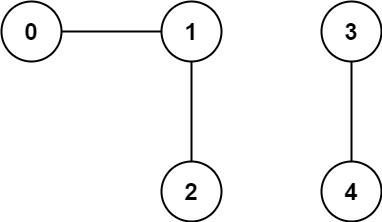
Input: n = 5, edges = [[0,1],[1,2],[3,4]]
Output: 2
Example 2:
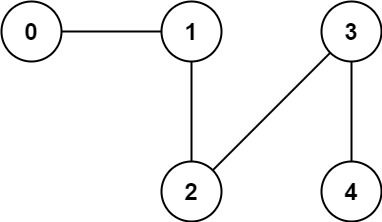
Input: n = 5, edges = [[0,1],[1,2],[2,3],[3,4]]
Output: 1
Constraints:
1 <= n <= 20001 <= edges.length <= 5000edges[i].length == 20 <= ai <= bi < nai != bi There are no repeated edges.
Solutions
Solution 1: DFS
First, we construct an adjacency list \(g\) based on the given edges, where \(g[i]\) represents all neighbor nodes of node \(i\) .
Then we traverse all nodes. For each node, we use DFS to traverse all its adjacent nodes and mark them as visited until all its adjacent nodes have been visited. In this way, we have found a connected component, and the answer is incremented by one. Then we continue to traverse the next unvisited node until all nodes have been visited.
The time complexity is \(O(n + m)\) , and the space complexity is \(O(n + m)\) . Where \(n\) and \(m\) are the number of nodes and edges, respectively.
Python3 Java C++ Go TypeScript JavaScript
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16 class Solution :
def countComponents ( self , n : int , edges : List [ List [ int ]]) -> int :
def dfs ( i : int ) -> int :
if i in vis :
return 0
vis . add ( i )
for j in g [ i ]:
dfs ( j )
return 1
g = [[] for _ in range ( n )]
for a , b in edges :
g [ a ] . append ( b )
g [ b ] . append ( a )
vis = set ()
return sum ( dfs ( i ) for i in range ( n ))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31 class Solution {
private List < Integer >[] g ;
private boolean [] vis ;
public int countComponents ( int n , int [][] edges ) {
g = new List [ n ] ;
vis = new boolean [ n ] ;
Arrays . setAll ( g , k -> new ArrayList <> ());
for ( var e : edges ) {
int a = e [ 0 ] , b = e [ 1 ] ;
g [ a ] . add ( b );
g [ b ] . add ( a );
}
int ans = 0 ;
for ( int i = 0 ; i < n ; ++ i ) {
ans += dfs ( i );
}
return ans ;
}
private int dfs ( int i ) {
if ( vis [ i ] ) {
return 0 ;
}
vis [ i ] = true ;
for ( int j : g [ i ] ) {
dfs ( j );
}
return 1 ;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27 class Solution {
public :
int countComponents ( int n , vector < vector < int >>& edges ) {
vector < int > g [ n ];
for ( auto & e : edges ) {
int a = e [ 0 ], b = e [ 1 ];
g [ a ]. push_back ( b );
g [ b ]. push_back ( a );
}
vector < bool > vis ( n );
function < int ( int ) > dfs = [ & ]( int i ) {
if ( vis [ i ]) {
return 0 ;
}
vis [ i ] = true ;
for ( int j : g [ i ]) {
dfs ( j );
}
return 1 ;
};
int ans = 0 ;
for ( int i = 0 ; i < n ; ++ i ) {
ans += dfs ( i );
}
return ans ;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24 func countComponents ( n int , edges [][] int ) ( ans int ) {
g := make ([][] int , n )
for _ , e := range edges {
a , b := e [ 0 ], e [ 1 ]
g [ a ] = append ( g [ a ], b )
g [ b ] = append ( g [ b ], a )
}
vis := make ([] bool , n )
var dfs func ( int ) int
dfs = func ( i int ) int {
if vis [ i ] {
return 0
}
vis [ i ] = true
for _ , j := range g [ i ] {
dfs ( j )
}
return 1
}
for i := range g {
ans += dfs ( i )
}
return
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19 function countComponents ( n : number , edges : number [][]) : number {
const g : number [][] = Array . from ({ length : n }, () => []);
for ( const [ a , b ] of edges ) {
g [ a ]. push ( b );
g [ b ]. push ( a );
}
const vis : boolean [] = Array ( n ). fill ( false );
const dfs = ( i : number ) : number => {
if ( vis [ i ]) {
return 0 ;
}
vis [ i ] = true ;
for ( const j of g [ i ]) {
dfs ( j );
}
return 1 ;
};
return g . reduce (( acc , _ , i ) => acc + dfs ( i ), 0 );
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24 /**
* @param {number} n
* @param {number[][]} edges
* @return {number}
*/
var countComponents = function ( n , edges ) {
const g = Array . from ({ length : n }, () => []);
for ( const [ a , b ] of edges ) {
g [ a ]. push ( b );
g [ b ]. push ( a );
}
const vis = Array ( n ). fill ( false );
const dfs = i => {
if ( vis [ i ]) {
return 0 ;
}
vis [ i ] = true ;
for ( const j of g [ i ]) {
dfs ( j );
}
return 1 ;
};
return g . reduce (( acc , _ , i ) => acc + dfs ( i ), 0 );
};
Solution 2: Union-Find
We can use a union-find set to maintain the connected components in the graph.
First, we initialize a union-find set, then traverse all the edges. For each edge \((a, b)\) , we merge nodes \(a\) and \(b\) into the same connected component. If the merge is successful, it means that nodes \(a\) and \(b\) were not in the same connected component before, and the number of connected components decreases by one.
Finally, we return the number of connected components.
The time complexity is \(O(n + m \times \alpha(n))\) , and the space complexity is \(O(n)\) . Where \(n\) and \(m\) are the number of nodes and edges, respectively, and \(\alpha(n)\) is the inverse of the Ackermann function, which can be regarded as a very small constant.
Python3 Java C++ Go TypeScript
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29 class UnionFind :
def __init__ ( self , n ):
self . p = list ( range ( n ))
self . size = [ 1 ] * n
def find ( self , x ):
if self . p [ x ] != x :
self . p [ x ] = self . find ( self . p [ x ])
return self . p [ x ]
def union ( self , a , b ):
pa , pb = self . find ( a ), self . find ( b )
if pa == pb :
return False
if self . size [ pa ] > self . size [ pb ]:
self . p [ pb ] = pa
self . size [ pa ] += self . size [ pb ]
else :
self . p [ pa ] = pb
self . size [ pb ] += self . size [ pa ]
return True
class Solution :
def countComponents ( self , n : int , edges : List [ List [ int ]]) -> int :
uf = UnionFind ( n )
for a , b in edges :
n -= uf . union ( a , b )
return n
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45 class UnionFind {
private final int [] p ;
private final int [] size ;
public UnionFind ( int n ) {
p = new int [ n ] ;
size = new int [ n ] ;
for ( int i = 0 ; i < n ; ++ i ) {
p [ i ] = i ;
size [ i ] = 1 ;
}
}
public int find ( int x ) {
if ( p [ x ] != x ) {
p [ x ] = find ( p [ x ] );
}
return p [ x ] ;
}
public boolean union ( int a , int b ) {
int pa = find ( a ), pb = find ( b );
if ( pa == pb ) {
return false ;
}
if ( size [ pa ] > size [ pb ] ) {
p [ pb ] = pa ;
size [ pa ] += size [ pb ] ;
} else {
p [ pa ] = pb ;
size [ pb ] += size [ pa ] ;
}
return true ;
}
}
class Solution {
public int countComponents ( int n , int [][] edges ) {
UnionFind uf = new UnionFind ( n );
for ( var e : edges ) {
n -= uf . union ( e [ 0 ] , e [ 1 ] ) ? 1 : 0 ;
}
return n ;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44 class UnionFind {
public :
UnionFind ( int n ) {
p = vector < int > ( n );
size = vector < int > ( n , 1 );
iota ( p . begin (), p . end (), 0 );
}
bool unite ( int a , int b ) {
int pa = find ( a ), pb = find ( b );
if ( pa == pb ) {
return false ;
}
if ( size [ pa ] > size [ pb ]) {
p [ pb ] = pa ;
size [ pa ] += size [ pb ];
} else {
p [ pa ] = pb ;
size [ pb ] += size [ pa ];
}
return true ;
}
int find ( int x ) {
if ( p [ x ] != x ) {
p [ x ] = find ( p [ x ]);
}
return p [ x ];
}
private :
vector < int > p , size ;
};
class Solution {
public :
int countComponents ( int n , vector < vector < int >>& edges ) {
UnionFind uf ( n );
for ( auto & e : edges ) {
n -= uf . unite ( e [ 0 ], e [ 1 ]);
}
return n ;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45 type unionFind struct {
p , size [] int
}
func newUnionFind ( n int ) * unionFind {
p := make ([] int , n )
size := make ([] int , n )
for i := range p {
p [ i ] = i
size [ i ] = 1
}
return & unionFind { p , size }
}
func ( uf * unionFind ) find ( x int ) int {
if uf . p [ x ] != x {
uf . p [ x ] = uf . find ( uf . p [ x ])
}
return uf . p [ x ]
}
func ( uf * unionFind ) union ( a , b int ) bool {
pa , pb := uf . find ( a ), uf . find ( b )
if pa == pb {
return false
}
if uf . size [ pa ] > uf . size [ pb ] {
uf . p [ pb ] = pa
uf . size [ pa ] += uf . size [ pb ]
} else {
uf . p [ pa ] = pb
uf . size [ pb ] += uf . size [ pa ]
}
return true
}
func countComponents ( n int , edges [][] int ) int {
uf := newUnionFind ( n )
for _ , e := range edges {
if uf . union ( e [ 0 ], e [ 1 ]) {
n --
}
}
return n
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40 class UnionFind {
p : number [];
size : number [];
constructor ( n : number ) {
this . p = Array ( n )
. fill ( 0 )
. map (( _ , i ) => i );
this . size = Array ( n ). fill ( 1 );
}
find ( x : number ) : number {
if ( this . p [ x ] !== x ) {
this . p [ x ] = this . find ( this . p [ x ]);
}
return this . p [ x ];
}
union ( a : number , b : number ) : boolean {
const [ pa , pb ] = [ this . find ( a ), this . find ( b )];
if ( pa === pb ) {
return false ;
}
if ( this . size [ pa ] > this . size [ pb ]) {
this . p [ pb ] = pa ;
this . size [ pa ] += this . size [ pb ];
} else {
this . p [ pa ] = pb ;
this . size [ pb ] += this . size [ pa ];
}
return true ;
}
}
function countComponents ( n : number , edges : number [][]) : number {
const uf = new UnionFind ( n );
for ( const [ a , b ] of edges ) {
n -= uf . union ( a , b ) ? 1 : 0 ;
}
return n ;
}
Solution 3: BFS
We can also use BFS (Breadth-First Search) to count the number of connected components in the graph.
Similar to Solution 1, we first construct an adjacency list \(g\) based on the given edges. Then we traverse all nodes. For each node, if it has not been visited, we start BFS traversal from this node, marking all its adjacent nodes as visited, until all its adjacent nodes have been visited. In this way, we have found a connected component, and the answer is incremented by one.
After traversing all nodes, we get the number of connected components in the graph.
The time complexity is \(O(n + m)\) , and the space complexity is \(O(n + m)\) . Where \(n\) and \(m\) are the number of nodes and edges, respectively.
Python3 Java C++ Go TypeScript
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21 class Solution :
def countComponents ( self , n : int , edges : List [ List [ int ]]) -> int :
g = [[] for _ in range ( n )]
for a , b in edges :
g [ a ] . append ( b )
g [ b ] . append ( a )
vis = set ()
ans = 0
for i in range ( n ):
if i in vis :
continue
vis . add ( i )
q = deque ([ i ])
while q :
a = q . popleft ()
for b in g [ a ]:
if b not in vis :
vis . add ( b )
q . append ( b )
ans += 1
return ans
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32 class Solution {
public int countComponents ( int n , int [][] edges ) {
List < Integer >[] g = new List [ n ] ;
Arrays . setAll ( g , k -> new ArrayList <> ());
for ( var e : edges ) {
int a = e [ 0 ] , b = e [ 1 ] ;
g [ a ] . add ( b );
g [ b ] . add ( a );
}
int ans = 0 ;
boolean [] vis = new boolean [ n ] ;
for ( int i = 0 ; i < n ; ++ i ) {
if ( vis [ i ] ) {
continue ;
}
vis [ i ] = true ;
++ ans ;
Deque < Integer > q = new ArrayDeque <> ();
q . offer ( i );
while ( ! q . isEmpty ()) {
int a = q . poll ();
for ( int b : g [ a ] ) {
if ( ! vis [ b ] ) {
vis [ b ] = true ;
q . offer ( b );
}
}
}
}
return ans ;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32 class Solution {
public :
int countComponents ( int n , vector < vector < int >>& edges ) {
vector < int > g [ n ];
for ( auto & e : edges ) {
int a = e [ 0 ], b = e [ 1 ];
g [ a ]. push_back ( b );
g [ b ]. push_back ( a );
}
vector < bool > vis ( n );
int ans = 0 ;
for ( int i = 0 ; i < n ; ++ i ) {
if ( vis [ i ]) {
continue ;
}
vis [ i ] = true ;
++ ans ;
queue < int > q {{ i }};
while ( ! q . empty ()) {
int a = q . front ();
q . pop ();
for ( int b : g [ a ]) {
if ( ! vis [ b ]) {
vis [ b ] = true ;
q . push ( b );
}
}
}
}
return ans ;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28 func countComponents ( n int , edges [][] int ) ( ans int ) {
g := make ([][] int , n )
for _ , e := range edges {
a , b := e [ 0 ], e [ 1 ]
g [ a ] = append ( g [ a ], b )
g [ b ] = append ( g [ b ], a )
}
vis := make ([] bool , n )
for i := range g {
if vis [ i ] {
continue
}
vis [ i ] = true
ans ++
q := [] int { i }
for len ( q ) > 0 {
a := q [ 0 ]
q = q [ 1 :]
for _ , b := range g [ a ] {
if ! vis [ b ] {
vis [ b ] = true
q = append ( q , b )
}
}
}
}
return
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25 function countComponents ( n : number , edges : number [][]) : number {
const g : Map < number , number [] > = new Map ( Array . from ({ length : n }, ( _ , i ) => [ i , []]));
for ( const [ a , b ] of edges ) {
g . get ( a ) ! . push ( b );
g . get ( b ) ! . push ( a );
}
const vis = new Set < number > ();
let ans = 0 ;
for ( const [ i ] of g ) {
if ( vis . has ( i )) {
continue ;
}
const q = [ i ];
for ( const j of q ) {
if ( vis . has ( j )) {
continue ;
}
vis . add ( j );
q . push (... g . get ( j ) ! );
}
ans ++ ;
}
return ans ;
}