3218. Minimum Cost for Cutting Cake I

Description

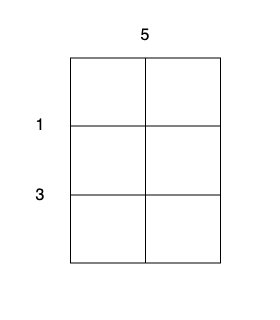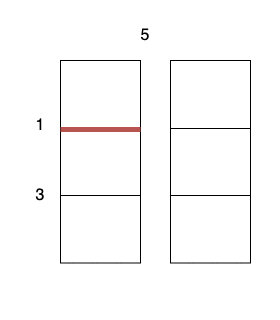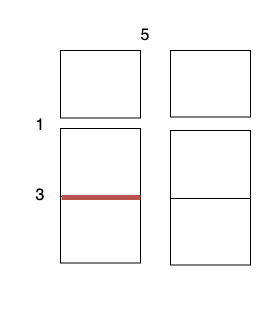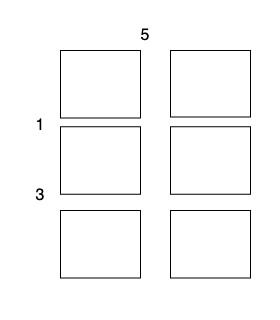
There is an m x n cake that needs to be cut into 1 x 1 pieces.

You are given integers m, n, and two arrays:

• horizontalCut of size m - 1, where horizontalCut[i] represents the cost to cut along the horizontal line i.
• verticalCut of size n - 1, where verticalCut[j] represents the cost to cut along the vertical line j.

In one operation, you can choose any piece of cake that is not yet a 1 x 1 square and perform one of the following cuts:

1. Cut along a horizontal line i at a cost of horizontalCut[i].
2. Cut along a vertical line j at a cost of verticalCut[j].

After the cut, the piece of cake is divided into two distinct pieces.

The cost of a cut depends only on the initial cost of the line and does not change.

Return the minimum total cost to cut the entire cake into 1 x 1 pieces.

 

Example 1:

Input: m = 3, n = 2, horizontalCut = [1,3], verticalCut = [5]

Output: 13

Explanation:

• Perform a cut on the vertical line 0 with cost 5, current total cost is 5.
• Perform a cut on the horizontal line 0 on 3 x 1 subgrid with cost 1.
• Perform a cut on the horizontal line 0 on 3 x 1 subgrid with cost 1.
• Perform a cut on the horizontal line 1 on 2 x 1 subgrid with cost 3.
• Perform a cut on the horizontal line 1 on 2 x 1 subgrid with cost 3.

The total cost is 5 + 1 + 1 + 3 + 3 = 13.

Example 2:

Input: m = 2, n = 2, horizontalCut = [7], verticalCut = [4]

Output: 15

Explanation:

• Perform a cut on the horizontal line 0 with cost 7.
• Perform a cut on the vertical line 0 on 1 x 2 subgrid with cost 4.
• Perform a cut on the vertical line 0 on 1 x 2 subgrid with cost 4.

The total cost is 7 + 4 + 4 = 15.

 

Constraints:

• 1 <= m, n <= 20
• horizontalCut.length == m - 1
• verticalCut.length == n - 1
• 1 <= horizontalCut[i], verticalCut[i] <= 103

Solutions

Solution 1: Greedy + Two Pointers

For a given position, the earlier you cut, the fewer cuts are needed, so it is clear that positions with higher costs should be cut earlier.

Therefore, we can sort the arrays $\textit{horizontalCut}$ and $\textit{verticalCut}$ in descending order, and then use two pointers $i$ and $j$ to point to the costs in $\textit{horizontalCut}$ and $\textit{verticalCut}$, respectively. Each time, we choose the position with the larger cost to cut, while updating the corresponding number of rows and columns.

Each time a horizontal cut is made, if the number of columns before the cut was $v$, then the cost of this cut is $\textit{horizontalCut}[i] \times v$, and then the number of rows $h$ is incremented by one; similarly, each time a vertical cut is made, if the number of rows before the cut was $h$, then the cost of this cut is $\textit{verticalCut}[j] \times h$, and then the number of columns $v$ is incremented by one.

Finally, when both $i$ and $j$ reach the end, return the total cost.

The time complexity is $O(m \times \log m + n \times \log n)$, and the space complexity is $O(\log m + \log n)$. Here, $m$ and $n$ are the lengths of $\textit{horizontalCut}$ and $\textit{verticalCut}$, respectively.

Python3JavaC++GoTypeScript

class Solution:
    def minimumCost(
        self, m: int, n: int, horizontalCut: List[int], verticalCut: List[int]
    ) -> int:
        horizontalCut.sort(reverse=True)
        verticalCut.sort(reverse=True)
        ans = i = j = 0
        h = v = 1
        while i < m - 1 or j < n - 1:
            if j == n - 1 or (i < m - 1 and horizontalCut[i] > verticalCut[j]):
                ans += horizontalCut[i] * v
                h, i = h + 1, i + 1
            else:
                ans += verticalCut[j] * h
                v, j = v + 1, j + 1
        return ans

class Solution {
    public int minimumCost(int m, int n, int[] horizontalCut, int[] verticalCut) {
        Arrays.sort(horizontalCut);
        Arrays.sort(verticalCut);
        int ans = 0;
        int i = m - 2, j = n - 2;
        int h = 1, v = 1;
        while (i >= 0 || j >= 0) {
            if (j < 0 || (i >= 0 && horizontalCut[i] > verticalCut[j])) {
                ans += horizontalCut[i--] * v;
                ++h;
            } else {
                ans += verticalCut[j--] * h;
                ++v;
            }
        }
        return ans;
    }
}

class Solution {
public:
    int minimumCost(int m, int n, vector<int>& horizontalCut, vector<int>& verticalCut) {
        sort(horizontalCut.rbegin(), horizontalCut.rend());
        sort(verticalCut.rbegin(), verticalCut.rend());
        int ans = 0;
        int i = 0, j = 0;
        int h = 1, v = 1;
        while (i < m - 1 || j < n - 1) {
            if (j == n - 1 || (i < m - 1 && horizontalCut[i] > verticalCut[j])) {
                ans += horizontalCut[i++] * v;
                h++;
            } else {
                ans += verticalCut[j++] * h;
                v++;
            }
        }
        return ans;
    }
};

func minimumCost(m int, n int, horizontalCut []int, verticalCut []int) (ans int) {
    sort.Sort(sort.Reverse(sort.IntSlice(horizontalCut)))
    sort.Sort(sort.Reverse(sort.IntSlice(verticalCut)))
    i, j := 0, 0
    h, v := 1, 1
    for i < m-1 || j < n-1 {
        if j == n-1 || (i < m-1 && horizontalCut[i] > verticalCut[j]) {
            ans += horizontalCut[i] * v
            h++
            i++
        } else {
            ans += verticalCut[j] * h
            v++
            j++
        }
    }
    return
}

function minimumCost(m: number, n: number, horizontalCut: number[], verticalCut: number[]): number {
    horizontalCut.sort((a, b) => b - a);
    verticalCut.sort((a, b) => b - a);
    let ans = 0;
    let [i, j] = [0, 0];
    let [h, v] = [1, 1];
    while (i < m - 1 || j < n - 1) {
        if (j === n - 1 || (i < m - 1 && horizontalCut[i] > verticalCut[j])) {
            ans += horizontalCut[i] * v;
            h++;
            i++;
        } else {
            ans += verticalCut[j] * h;
            v++;
            j++;
        }
    }
    return ans;
}

Comments