Skip to content

3208. Alternating Groups II

Description

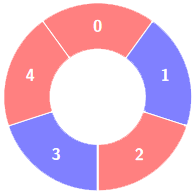
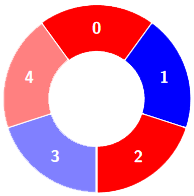
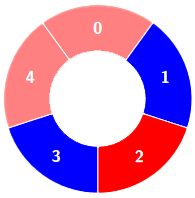
There is a circle of red and blue tiles. You are given an array of integers colors and an integer k. The color of tile i is represented by colors[i]:

  • colors[i] == 0 means that tile i is red.
  • colors[i] == 1 means that tile i is blue.

An alternating group is every k contiguous tiles in the circle with alternating colors (each tile in the group except the first and last one has a different color from its left and right tiles).

Return the number of alternating groups.

Note that since colors represents a circle, the first and the last tiles are considered to be next to each other.

 

Example 1:

Input: colors = [0,1,0,1,0], k = 3

Output: 3

Explanation:

Alternating groups:

Example 2:

Input: colors = [0,1,0,0,1,0,1], k = 6

Output: 2

Explanation:

Alternating groups:

Example 3:

Input: colors = [1,1,0,1], k = 4

Output: 0

Explanation:

 

Constraints:

  • 3 <= colors.length <= 105
  • 0 <= colors[i] <= 1
  • 3 <= k <= colors.length

Solutions

Solution 1: Single Pass

We can unfold the ring into an array of length $2n$ and then traverse this array from left to right. We use a variable $\textit{cnt}$ to record the current length of the alternating group. If we encounter the same color, we reset $\textit{cnt}$ to $1$; otherwise, we increment $\textit{cnt}$. If $\textit{cnt} \ge k$ and the current position $i$ is greater than or equal to $n$, then we have found an alternating group, and we increment the answer by one.

After the traversal, we return the answer.

The time complexity is $O(n)$, where $n$ is the length of the array $\textit{colors}$. The space complexity is $O(1)$.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
class Solution:
    def numberOfAlternatingGroups(self, colors: List[int], k: int) -> int:
        n = len(colors)
        ans = cnt = 0
        for i in range(n << 1):
            if i and colors[i % n] == colors[(i - 1) % n]:
                cnt = 1
            else:
                cnt += 1
            ans += i >= n and cnt >= k
        return ans

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
class Solution {
    public int numberOfAlternatingGroups(int[] colors, int k) {
        int n = colors.length;
        int ans = 0, cnt = 0;
        for (int i = 0; i < n << 1; ++i) {
            if (i > 0 && colors[i % n] == colors[(i - 1) % n]) {
                cnt = 1;
            } else {
                ++cnt;
            }
            ans += i >= n && cnt >= k ? 1 : 0;
        }
        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
class Solution {
public:
    int numberOfAlternatingGroups(vector<int>& colors, int k) {
        int n = colors.size();
        int ans = 0, cnt = 0;
        for (int i = 0; i < n << 1; ++i) {
            if (i && colors[i % n] == colors[(i - 1) % n]) {
                cnt = 1;
            } else {
                ++cnt;
            }
            ans += i >= n && cnt >= k ? 1 : 0;
        }
        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
func numberOfAlternatingGroups(colors []int, k int) (ans int) {
    n := len(colors)
    cnt := 0
    for i := 0; i < n<<1; i++ {
        if i > 0 && colors[i%n] == colors[(i-1)%n] {
            cnt = 1
        } else {
            cnt++
        }
        if i >= n && cnt >= k {
            ans++
        }
    }
    return
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
function numberOfAlternatingGroups(colors: number[], k: number): number {
    const n = colors.length;
    let [ans, cnt] = [0, 0];
    for (let i = 0; i < n << 1; ++i) {
        if (i && colors[i % n] === colors[(i - 1) % n]) {
            cnt = 1;
        } else {
            ++cnt;
        }
        ans += i >= n && cnt >= k ? 1 : 0;
    }
    return ans;
}

Comments