Skip to content

3206. Alternating Groups I

Description

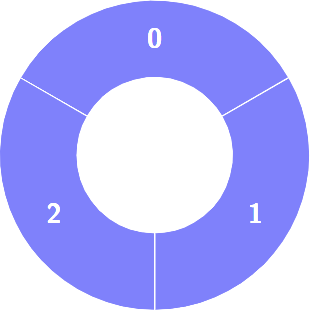
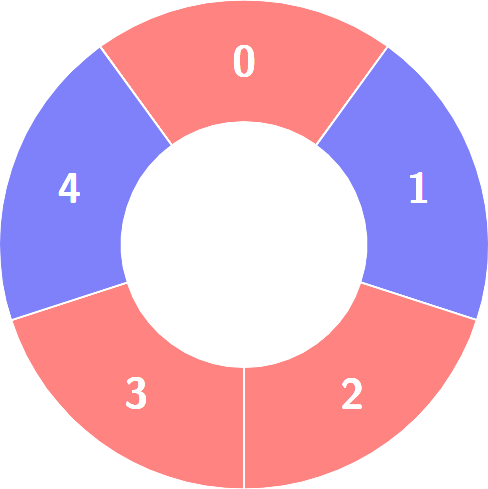
There is a circle of red and blue tiles. You are given an array of integers colors. The color of tile i is represented by colors[i]:

  • colors[i] == 0 means that tile i is red.
  • colors[i] == 1 means that tile i is blue.

Every 3 contiguous tiles in the circle with alternating colors (the middle tile has a different color from its left and right tiles) is called an alternating group.

Return the number of alternating groups.

Note that since colors represents a circle, the first and the last tiles are considered to be next to each other.

 

Example 1:

Input: colors = [1,1,1]

Output: 0

Explanation:

Example 2:

Input: colors = [0,1,0,0,1]

Output: 3

Explanation:

Alternating groups:

 

Constraints:

  • 3 <= colors.length <= 100
  • 0 <= colors[i] <= 1

Solutions

Solution 1: Single Pass

We set \(k = 3\), indicating that the length of the alternating group is \(3\).

For convenience, we can unfold the ring into an array of length \(2n\) and then traverse this array from left to right. We use a variable \(\textit{cnt}\) to record the current length of the alternating group. If we encounter the same color, we reset \(\textit{cnt}\) to \(1\); otherwise, we increment \(\textit{cnt}\). If \(\textit{cnt} \ge k\) and the current position \(i\) is greater than or equal to \(n\), then we have found an alternating group, and we increment the answer by one.

After the traversal, we return the answer.

The time complexity is \(O(n)\), where \(n\) is the length of the array \(\textit{colors}\). The space complexity is \(O(1)\).

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
class Solution:
    def numberOfAlternatingGroups(self, colors: List[int]) -> int:
        k = 3
        n = len(colors)
        ans = cnt = 0
        for i in range(n << 1):
            if i and colors[i % n] == colors[(i - 1) % n]:
                cnt = 1
            else:
                cnt += 1
            ans += i >= n and cnt >= k
        return ans

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
class Solution {
    public int numberOfAlternatingGroups(int[] colors) {
        int k = 3;
        int n = colors.length;
        int ans = 0, cnt = 0;
        for (int i = 0; i < n << 1; ++i) {
            if (i > 0 && colors[i % n] == colors[(i - 1) % n]) {
                cnt = 1;
            } else {
                ++cnt;
            }
            ans += i >= n && cnt >= k ? 1 : 0;
        }
        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
class Solution {
public:
    int numberOfAlternatingGroups(vector<int>& colors) {
        int k = 3;
        int n = colors.size();
        int ans = 0, cnt = 0;
        for (int i = 0; i < n << 1; ++i) {
            if (i && colors[i % n] == colors[(i - 1) % n]) {
                cnt = 1;
            } else {
                ++cnt;
            }
            ans += i >= n && cnt >= k ? 1 : 0;
        }
        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
func numberOfAlternatingGroups(colors []int) (ans int) {
    k := 3
    n := len(colors)
    cnt := 0
    for i := 0; i < n<<1; i++ {
        if i > 0 && colors[i%n] == colors[(i-1)%n] {
            cnt = 1
        } else {
            cnt++
        }
        if i >= n && cnt >= k {
            ans++
        }
    }
    return
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
function numberOfAlternatingGroups(colors: number[]): number {
    const k = 3;
    const n = colors.length;
    let [ans, cnt] = [0, 0];
    for (let i = 0; i < n << 1; ++i) {
        if (i && colors[i % n] === colors[(i - 1) % n]) {
            cnt = 1;
        } else {
            ++cnt;
        }
        ans += i >= n && cnt >= k ? 1 : 0;
    }
    return ans;
}

Comments