3203. Find Minimum Diameter After Merging Two Trees

Description

There exist two undirected trees with n and m nodes, numbered from 0 to n - 1 and from 0 to m - 1, respectively. You are given two 2D integer arrays edges1 and edges2 of lengths n - 1 and m - 1, respectively, where edges1[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the first tree and edges2[i] = [ui, vi] indicates that there is an edge between nodes ui and vi in the second tree.

You must connect one node from the first tree with another node from the second tree with an edge.

Return the minimum possible diameter of the resulting tree.

The diameter of a tree is the length of the longest path between any two nodes in the tree.

 

Example 1:

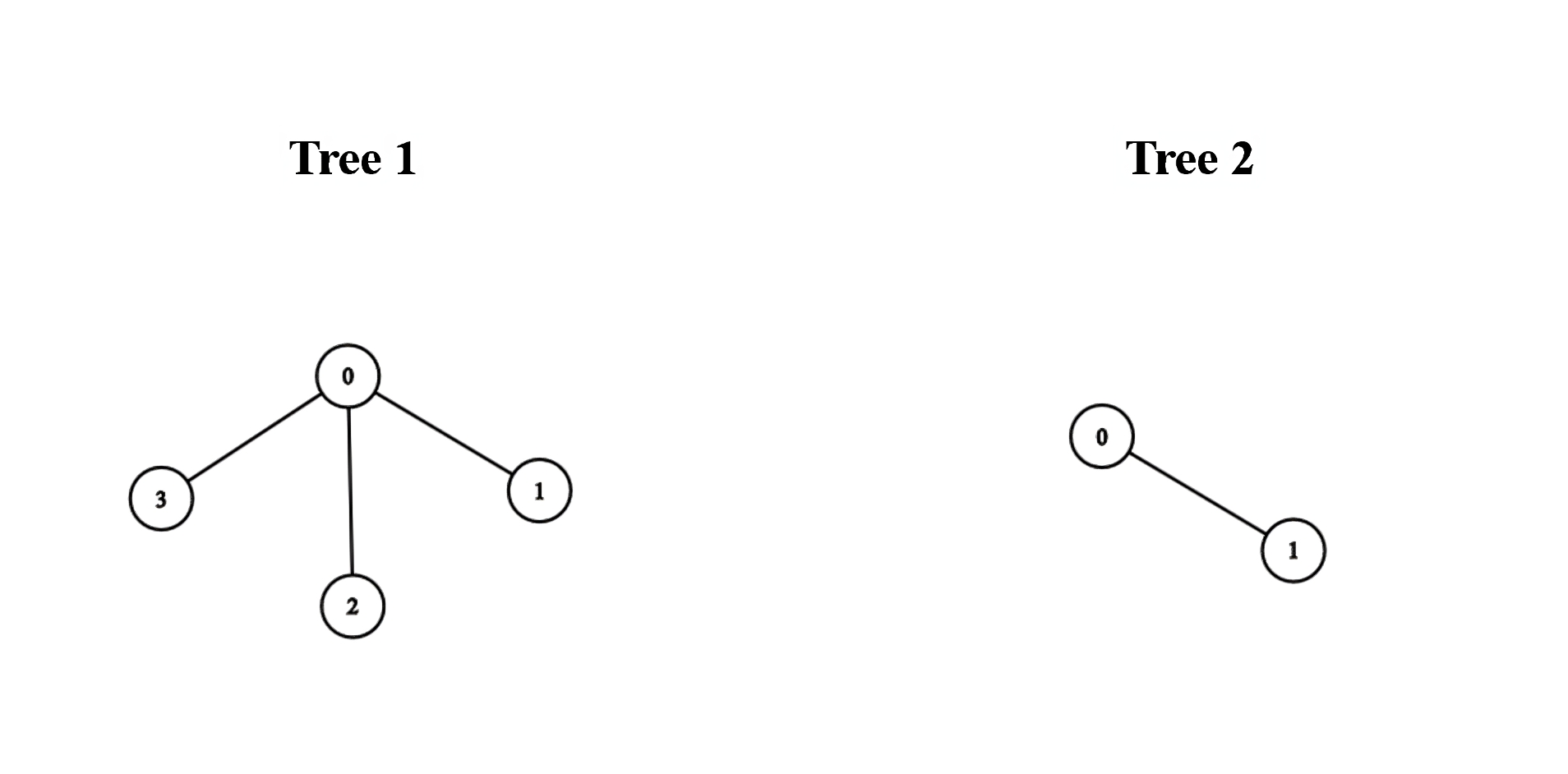
Input: edges1 = [[0,1],[0,2],[0,3]], edges2 = [[0,1]]

Output: 3

Explanation:

We can obtain a tree of diameter 3 by connecting node 0 from the first tree with any node from the second tree.

Example 2:

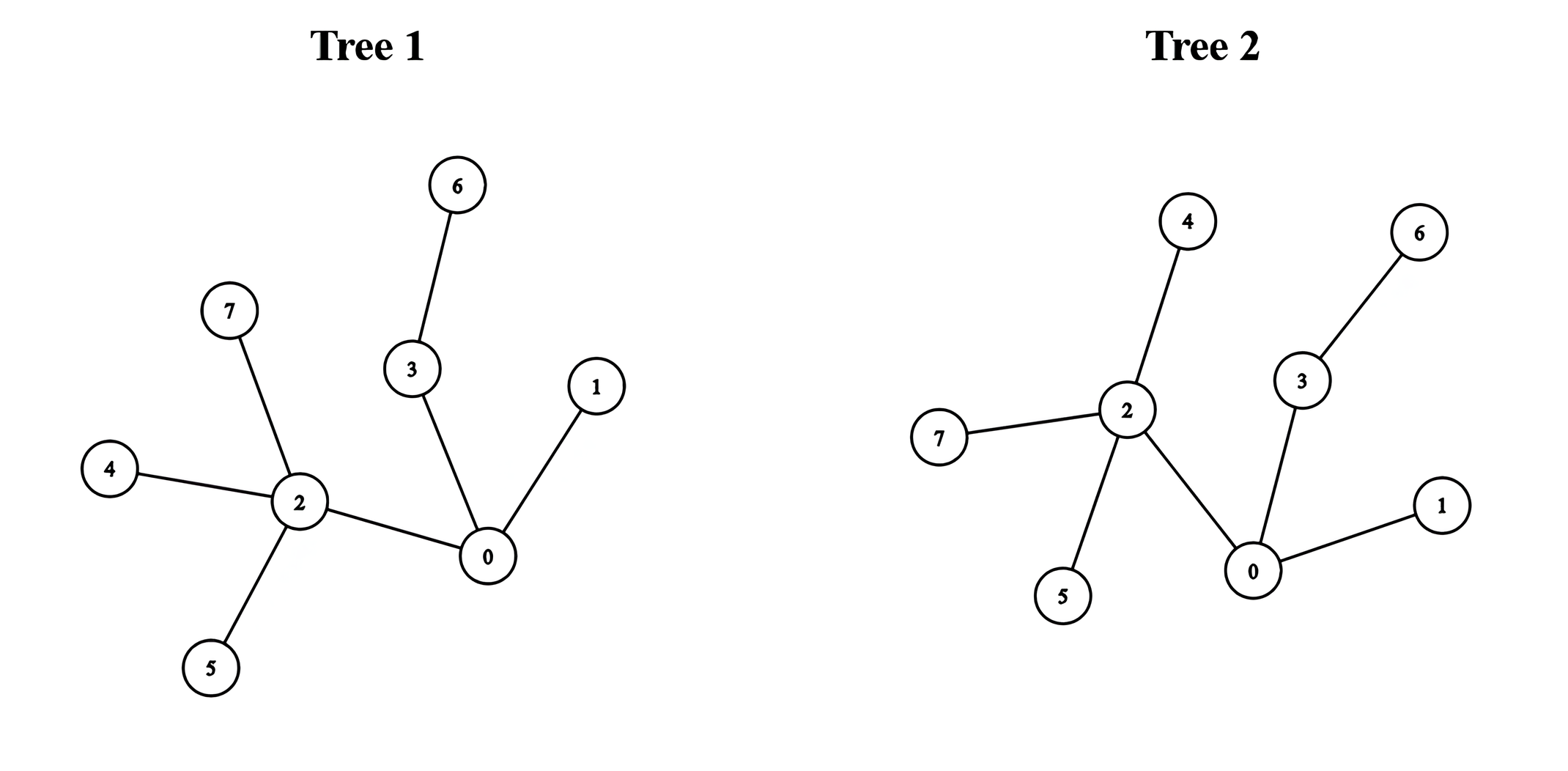
Input: edges1 = [[0,1],[0,2],[0,3],[2,4],[2,5],[3,6],[2,7]], edges2 = [[0,1],[0,2],[0,3],[2,4],[2,5],[3,6],[2,7]]

Output: 5

Explanation:

We can obtain a tree of diameter 5 by connecting node 0 from the first tree with node 0 from the second tree.

 

Constraints:

• 1 <= n, m <= 105
• edges1.length == n - 1
• edges2.length == m - 1
• edges1[i].length == edges2[i].length == 2
• edges1[i] = [ai, bi]
• 0 <= ai, bi < n
• edges2[i] = [ui, vi]
• 0 <= ui, vi < m
• The input is generated such that edges1 and edges2 represent valid trees.

Solutions

Solution 1: Two DFS Passes

We denote $d_1$ and $d_2$ as the diameters of the two trees, respectively. Then, the diameter of the merged tree can be one of the following two cases:

1. The diameter of the merged tree is the diameter of one of the original trees, i.e., $\max(d_1, d_2)$;
2. The diameter of the merged tree passes through both of the original trees. We calculate the radii of the original two trees as $r_1 = \lceil \frac{d_1}{2} \rceil$ and $r_2 = \lceil \frac{d_2}{2} \rceil$, respectively. Then, the diameter of the merged tree is $r_1 + r_2 + 1$.

We take the maximum of these two cases.

When calculating the diameter of a tree, we can use two DFS passes. First, we arbitrarily select a node and start a DFS from this node to find the farthest node from it, denoted as node $a$. Then, we start another DFS from node $a$ to find the farthest node from node $a$, denoted as node $b$. It can be proven that the path between node $a$ and node $b$ is the diameter of the tree.

The time complexity is $O(n + m)$, and the space complexity is $O(n + m)$, where $n$ and $m$ are the number of nodes in the two trees, respectively.

Python3JavaC++GoTypeScript

class Solution:
    def minimumDiameterAfterMerge(
        self, edges1: List[List[int]], edges2: List[List[int]]
    ) -> int:
        d1 = self.treeDiameter(edges1)
        d2 = self.treeDiameter(edges2)
        return max(d1, d2, (d1 + 1) // 2 + (d2 + 1) // 2 + 1)

    def treeDiameter(self, edges: List[List[int]]) -> int:
        def dfs(i: int, fa: int, t: int):
            for j in g[i]:
                if j != fa:
                    dfs(j, i, t + 1)
            nonlocal ans, a
            if ans < t:
                ans = t
                a = i

        g = defaultdict(list)
        for a, b in edges:
            g[a].append(b)
            g[b].append(a)
        ans = a = 0
        dfs(0, -1, 0)
        dfs(a, -1, 0)
        return ans

class Solution {
    private List<Integer>[] g;
    private int ans;
    private int a;

    public int minimumDiameterAfterMerge(int[][] edges1, int[][] edges2) {
        int d1 = treeDiameter(edges1);
        int d2 = treeDiameter(edges2);
        return Math.max(Math.max(d1, d2), (d1 + 1) / 2 + (d2 + 1) / 2 + 1);
    }

    public int treeDiameter(int[][] edges) {
        int n = edges.length + 1;
        g = new List[n];
        Arrays.setAll(g, k -> new ArrayList<>());
        ans = 0;
        a = 0;
        for (var e : edges) {
            int a = e[0], b = e[1];
            g[a].add(b);
            g[b].add(a);
        }
        dfs(0, -1, 0);
        dfs(a, -1, 0);
        return ans;
    }

    private void dfs(int i, int fa, int t) {
        for (int j : g[i]) {
            if (j != fa) {
                dfs(j, i, t + 1);
            }
        }
        if (ans < t) {
            ans = t;
            a = i;
        }
    }
}

class Solution {
public:
    int minimumDiameterAfterMerge(vector<vector<int>>& edges1, vector<vector<int>>& edges2) {
        int d1 = treeDiameter(edges1);
        int d2 = treeDiameter(edges2);
        return max({d1, d2, (d1 + 1) / 2 + (d2 + 1) / 2 + 1});
    }

    int treeDiameter(vector<vector<int>>& edges) {
        int n = edges.size() + 1;
        vector<int> g[n];
        for (auto& e : edges) {
            int a = e[0], b = e[1];
            g[a].push_back(b);
            g[b].push_back(a);
        }
        int ans = 0, a = 0;
        auto dfs = [&](this auto&& dfs, int i, int fa, int t) -> void {
            for (int j : g[i]) {
                if (j != fa) {
                    dfs(j, i, t + 1);
                }
            }
            if (ans < t) {
                ans = t;
                a = i;
            }
        };
        dfs(0, -1, 0);
        dfs(a, -1, 0);
        return ans;
    }
};

func minimumDiameterAfterMerge(edges1 [][]int, edges2 [][]int) int {
    d1 := treeDiameter(edges1)
    d2 := treeDiameter(edges2)
    return max(max(d1, d2), (d1+1)/2+(d2+1)/2+1)
}

func treeDiameter(edges [][]int) (ans int) {
    n := len(edges) + 1
    g := make([][]int, n)
    for _, e := range edges {
        a, b := e[0], e[1]
        g[a] = append(g[a], b)
        g[b] = append(g[b], a)
    }
    a := 0
    var dfs func(i, fa, t int)
    dfs = func(i, fa, t int) {
        for _, j := range g[i] {
            if j != fa {
                dfs(j, i, t+1)
            }
        }
        if ans < t {
            ans = t
            a = i
        }
    }
    dfs(0, -1, 0)
    dfs(a, -1, 0)
    return
}

function minimumDiameterAfterMerge(edges1: number[][], edges2: number[][]): number {
    const d1 = treeDiameter(edges1);
    const d2 = treeDiameter(edges2);
    return Math.max(d1, d2, Math.ceil(d1 / 2) + Math.ceil(d2 / 2) + 1);
}

function treeDiameter(edges: number[][]): number {
    const n = edges.length + 1;
    const g: number[][] = Array.from({ length: n }, () => []);
    for (const [a, b] of edges) {
        g[a].push(b);
        g[b].push(a);
    }
    let [ans, a] = [0, 0];
    const dfs = (i: number, fa: number, t: number): void => {
        for (const j of g[i]) {
            if (j !== fa) {
                dfs(j, i, t + 1);
            }
        }
        if (ans < t) {
            ans = t;
            a = i;
        }
    };
    dfs(0, -1, 0);
    dfs(a, -1, 0);
    return ans;
}

Comments