Skip to content

319. Bulb Switcher

Description

There are n bulbs that are initially off. You first turn on all the bulbs, then you turn off every second bulb.

On the third round, you toggle every third bulb (turning on if it's off or turning off if it's on). For the ith round, you toggle every i bulb. For the nth round, you only toggle the last bulb.

Return the number of bulbs that are on after n rounds.

 

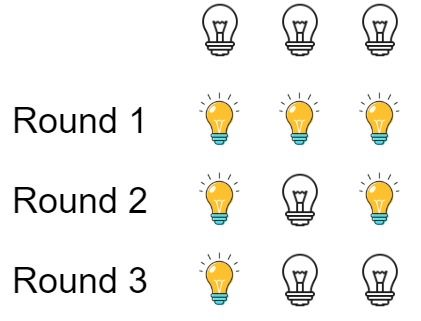
Example 1:

Input: n = 3
Output: 1
Explanation: At first, the three bulbs are [off, off, off].
After the first round, the three bulbs are [on, on, on].
After the second round, the three bulbs are [on, off, on].
After the third round, the three bulbs are [on, off, off]. 
So you should return 1 because there is only one bulb is on.

Example 2:

Input: n = 0
Output: 0

Example 3:

Input: n = 1
Output: 1

 

Constraints:

  • 0 <= n <= 109

Solutions

Solution 1: Mathematics

We can number the $n$ bulbs as $1, 2, 3, \cdots, n$. For the $i$-th bulb, it will be operated in the $d$-th round if and only if $d$ is a factor of $i$.

For a number $i$, the number of its factors is finite. If the number of factors is odd, the final state is on; otherwise, it is off.

Therefore, we only need to find the number of numbers from $1$ to $n$ with an odd number of factors.

For a number $i$, if it has a factor $d$, then it must have a factor $i/d$. Therefore, numbers with an odd number of factors must be perfect squares.

For example, the factors of the number $12$ are $1, 2, 3, 4, 6, 12$, and the number of factors is $6$, which is even. For the perfect square number $16$, the factors are $1, 2, 4, 8, 16$, and the number of factors is $5$, which is odd.

Therefore, we only need to find how many perfect squares there are from $1$ to $n$, which is $\lfloor \sqrt{n} \rfloor$.

The time complexity is $O(1)$, and the space complexity is $O(1)$.

1
2
3
class Solution:
    def bulbSwitch(self, n: int) -> int:
        return int(sqrt(n))

1
2
3
4
5
class Solution {
    public int bulbSwitch(int n) {
        return (int) Math.sqrt(n);
    }
}

1
2
3
4
5
6
class Solution {
public:
    int bulbSwitch(int n) {
        return (int) sqrt(n);
    }
};

1
2
3
func bulbSwitch(n int) int {
    return int(math.Sqrt(float64(n)))
}

1
2
3
function bulbSwitch(n: number): number {
    return Math.floor(Math.sqrt(n));
}

Comments