3161. Block Placement Queries
Description
There exists an infinite number line, with its origin at 0 and extending towards the positive x-axis.
You are given a 2D array queries, which contains two types of queries:
- For a query of type 1,
queries[i] = [1, x]. Build an obstacle at distancexfrom the origin. It is guaranteed that there is no obstacle at distancexwhen the query is asked. - For a query of type 2,
queries[i] = [2, x, sz]. Check if it is possible to place a block of sizeszanywhere in the range[0, x]on the line, such that the block entirely lies in the range[0, x]. A block cannot be placed if it intersects with any obstacle, but it may touch it. Note that you do not actually place the block. Queries are separate.
Return a boolean array results, where results[i] is true if you can place the block specified in the ith query of type 2, and false otherwise.
Example 1:
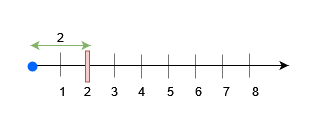
Input: queries = [[1,2],[2,3,3],[2,3,1],[2,2,2]]
Output: [false,true,true]
Explanation:
For query 0, place an obstacle at x = 2. A block of size at most 2 can be placed before x = 3.
Example 2:
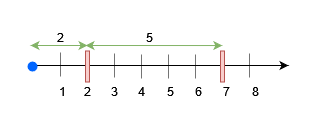
Input: queries = [[1,7],[2,7,6],[1,2],[2,7,5],[2,7,6]]
Output: [true,true,false]
Explanation:
- Place an obstacle at
x = 7for query 0. A block of size at most 7 can be placed beforex = 7. - Place an obstacle at
x = 2for query 2. Now, a block of size at most 5 can be placed beforex = 7, and a block of size at most 2 beforex = 2.
Constraints:
1 <= queries.length <= 15 * 1042 <= queries[i].length <= 31 <= queries[i][0] <= 21 <= x, sz <= min(5 * 104, 3 * queries.length)- The input is generated such that for queries of type 1, no obstacle exists at distance
xwhen the query is asked. - The input is generated such that there is at least one query of type 2.
Solutions
Solution 1
1 | |
1 | |
1 | |
1 | |