Skip to content

3160. Find the Number of Distinct Colors Among the Balls

Description

You are given an integer limit and a 2D array queries of size n x 2.

There are limit + 1 balls with distinct labels in the range [0, limit]. Initially, all balls are uncolored. For every query in queries that is of the form [x, y], you mark ball x with the color y. After each query, you need to find the number of colors among the balls.

Return an array result of length n, where result[i] denotes the number of colors after ith query.

Note that when answering a query, lack of a color will not be considered as a color.

 

Example 1:

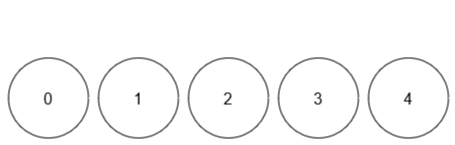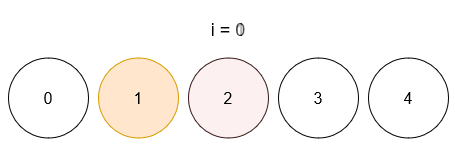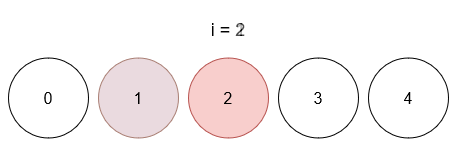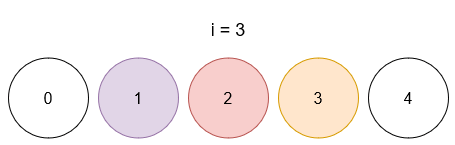
Input: limit = 4, queries = [[1,4],[2,5],[1,3],[3,4]]

Output: [1,2,2,3]

Explanation:

  • After query 0, ball 1 has color 4.
  • After query 1, ball 1 has color 4, and ball 2 has color 5.
  • After query 2, ball 1 has color 3, and ball 2 has color 5.
  • After query 3, ball 1 has color 3, ball 2 has color 5, and ball 3 has color 4.

Example 2:

Input: limit = 4, queries = [[0,1],[1,2],[2,2],[3,4],[4,5]]

Output: [1,2,2,3,4]

Explanation:

  • After query 0, ball 0 has color 1.
  • After query 1, ball 0 has color 1, and ball 1 has color 2.
  • After query 2, ball 0 has color 1, and balls 1 and 2 have color 2.
  • After query 3, ball 0 has color 1, balls 1 and 2 have color 2, and ball 3 has color 4.
  • After query 4, ball 0 has color 1, balls 1 and 2 have color 2, ball 3 has color 4, and ball 4 has color 5.

 

Constraints:

  • 1 <= limit <= 109
  • 1 <= n == queries.length <= 105
  • queries[i].length == 2
  • 0 <= queries[i][0] <= limit
  • 1 <= queries[i][1] <= 109

Solutions

Solution 1: Double Hash Tables

We use a hash table g to record the color of each ball, and another hash table cnt to record the count of each color.

Next, we traverse the array queries. For each query \((x, y)\), we increase the count of color \(y\) by \(1\), then check whether ball \(x\) has been colored. If it has, we decrease the count of the color of ball \(x\) by \(1\). If the count drops to \(0\), we remove it from the hash table cnt. Then, we update the color of ball \(x\) to \(y\), and add the current size of the hash table cnt to the answer array.

After the traversal, we return the answer array.

The time complexity is \(O(m)\), and the space complexity is \(O(m)\), where \(m\) is the length of the array queries.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
class Solution:
    def queryResults(self, limit: int, queries: List[List[int]]) -> List[int]:
        g = {}
        cnt = Counter()
        ans = []
        for x, y in queries:
            cnt[y] += 1
            if x in g:
                cnt[g[x]] -= 1
                if cnt[g[x]] == 0:
                    cnt.pop(g[x])
            g[x] = y
            ans.append(len(cnt))
        return ans

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
class Solution {
    public int[] queryResults(int limit, int[][] queries) {
        Map<Integer, Integer> g = new HashMap<>();
        Map<Integer, Integer> cnt = new HashMap<>();
        int m = queries.length;
        int[] ans = new int[m];
        for (int i = 0; i < m; ++i) {
            int x = queries[i][0], y = queries[i][1];
            cnt.merge(y, 1, Integer::sum);
            if (g.containsKey(x) && cnt.merge(g.get(x), -1, Integer::sum) == 0) {
                cnt.remove(g.get(x));
            }
            g.put(x, y);
            ans[i] = cnt.size();
        }
        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    vector<int> queryResults(int limit, vector<vector<int>>& queries) {
        unordered_map<int, int> g;
        unordered_map<int, int> cnt;
        vector<int> ans;
        for (auto& q : queries) {
            int x = q[0], y = q[1];
            cnt[y]++;
            if (g.contains(x) && --cnt[g[x]] == 0) {
                cnt.erase(g[x]);
            }
            g[x] = y;
            ans.push_back(cnt.size());
        }
        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
func queryResults(limit int, queries [][]int) (ans []int) {
    g := map[int]int{}
    cnt := map[int]int{}
    for _, q := range queries {
        x, y := q[0], q[1]
        cnt[y]++
        if v, ok := g[x]; ok {
            cnt[v]--
            if cnt[v] == 0 {
                delete(cnt, v)
            }
        }
        g[x] = y
        ans = append(ans, len(cnt))
    }
    return
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
function queryResults(limit: number, queries: number[][]): number[] {
    const g = new Map<number, number>();
    const cnt = new Map<number, number>();
    const ans: number[] = [];
    for (const [x, y] of queries) {
        cnt.set(y, (cnt.get(y) ?? 0) + 1);
        if (g.has(x)) {
            const v = g.get(x)!;
            cnt.set(v, cnt.get(v)! - 1);
            if (cnt.get(v) === 0) {
                cnt.delete(v);
            }
        }
        g.set(x, y);
        ans.push(cnt.size);
    }
    return ans;
}

Comments