Skip to content

3149. Find the Minimum Cost Array Permutation

Description

You are given an array nums which is a permutation of [0, 1, 2, ..., n - 1]. The score of any permutation of [0, 1, 2, ..., n - 1] named perm is defined as:

score(perm) = |perm[0] - nums[perm[1]]| + |perm[1] - nums[perm[2]]| + ... + |perm[n - 1] - nums[perm[0]]|

Return the permutation perm which has the minimum possible score. If multiple permutations exist with this score, return the one that is lexicographically smallest among them.

 

Example 1:

Input: nums = [1,0,2]

Output: [0,1,2]

Explanation:

The lexicographically smallest permutation with minimum cost is [0,1,2]. The cost of this permutation is |0 - 0| + |1 - 2| + |2 - 1| = 2.

Example 2:

Input: nums = [0,2,1]

Output: [0,2,1]

Explanation:

The lexicographically smallest permutation with minimum cost is [0,2,1]. The cost of this permutation is |0 - 1| + |2 - 2| + |1 - 0| = 2.

 

Constraints:

  • 2 <= n == nums.length <= 14
  • nums is a permutation of [0, 1, 2, ..., n - 1].

Solutions

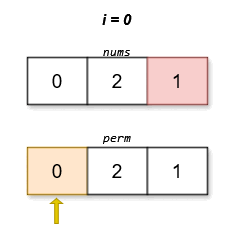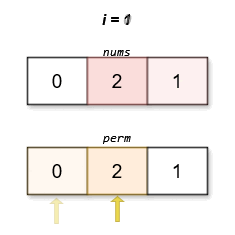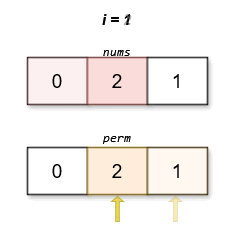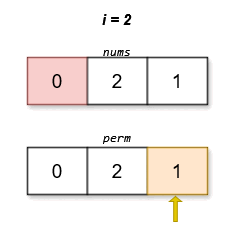
We notice that for any permutation $\textit{perm}$, if we cyclically shift it to the left any number of times, the score of the permutation remains the same. Since the problem requires returning the lexicographically smallest permutation, we can determine that the first element of the permutation must be $0$.

Also, since the data range of the problem does not exceed $14$, we can consider using the method of state compression to represent the set of numbers selected in the current permutation. We use a binary number $\textit{mask}$ of length $n$ to represent the set of numbers selected in the current permutation, where the $i$-th bit of $\textit{mask}$ is $1$ indicates that the number $i$ has been selected, and $0$ indicates that the number $i$ has not been selected yet.

We design a function $\textit{dfs}(\textit{mask}, \textit{pre})$, which represents the minimum score of the permutation obtained when the set of numbers selected in the current permutation is $\textit{mask}$ and the last selected number is $\textit{pre}$. Initially, we add the number $0$ to the permutation.

The calculation process of the function $\textit{dfs}(\textit{mask}, \textit{pre})$ is as follows:

  • If the number of $1$s in the binary representation of $\textit{mask}$ is $n$, that is, $\textit{mask} = 2^n - 1$, it means that all numbers have been selected, then return $|\textit{pre} - \textit{nums}[0]|$;
  • Otherwise, we enumerate the next selected number $\textit{cur}$. If the number $\textit{cur}$ has not been selected yet, then we can add the number $\textit{cur}$ to the permutation. At this time, the score of the permutation is $|\textit{pre} - \textit{nums}[\textit{cur}]| + \textit{dfs}(\textit{mask} \, | \, 1 << \textit{cur}, \textit{cur})$. We need to take the minimum score among all $\textit{cur}$.

Finally, we use a function $\textit{g}(\textit{mask}, \textit{pre})$ to construct the permutation that gets the minimum score. We first add the number $\textit{pre}$ to the permutation, and then enumerate the next selected number $\textit{cur}$. If the number $\textit{cur}$ has not been selected yet, and it satisfies that the value of $|\textit{pre} - \textit{nums}[\textit{cur}]| + \textit{dfs}(\textit{mask} \, | \, 1 << \textit{cur}, \textit{cur})$ is equal to $\textit{dfs}(\textit{mask}, \textit{pre})$, then we can add the number $\textit{cur}$ to the permutation.

The time complexity is $(n^2 \times 2^n)$, and the space complexity is $O(n \times 2^n)$. Where $n$ is the length of the array $\textit{nums}$.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution:
    def findPermutation(self, nums: List[int]) -> List[int]:
        @cache
        def dfs(mask: int, pre: int) -> int:
            if mask == (1 << n) - 1:
                return abs(pre - nums[0])
            res = inf
            for cur in range(1, n):
                if mask >> cur & 1 ^ 1:
                    res = min(res, abs(pre - nums[cur]) + dfs(mask | 1 << cur, cur))
            return res

        def g(mask: int, pre: int):
            ans.append(pre)
            if mask == (1 << n) - 1:
                return
            res = dfs(mask, pre)
            for cur in range(1, n):
                if mask >> cur & 1 ^ 1:
                    if abs(pre - nums[cur]) + dfs(mask | 1 << cur, cur) == res:
                        g(mask | 1 << cur, cur)
                        break

        n = len(nums)
        ans = []
        g(1, 0)
        return ans

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
class Solution {
    private Integer[][] f;
    private int[] nums;
    private int[] ans;
    private int n;

    public int[] findPermutation(int[] nums) {
        n = nums.length;
        ans = new int[n];
        this.nums = nums;
        f = new Integer[1 << n][n];
        g(1, 0, 0);
        return ans;
    }

    private int dfs(int mask, int pre) {
        if (mask == (1 << n) - 1) {
            return Math.abs(pre - nums[0]);
        }
        if (f[mask][pre] != null) {
            return f[mask][pre];
        }
        int res = Integer.MAX_VALUE;
        for (int cur = 1; cur < n; ++cur) {
            if ((mask >> cur & 1) == 0) {
                res = Math.min(res, Math.abs(pre - nums[cur]) + dfs(mask | 1 << cur, cur));
            }
        }
        return f[mask][pre] = res;
    }

    private void g(int mask, int pre, int k) {
        ans[k] = pre;
        if (mask == (1 << n) - 1) {
            return;
        }
        int res = dfs(mask, pre);
        for (int cur = 1; cur < n; ++cur) {
            if ((mask >> cur & 1) == 0) {
                if (Math.abs(pre - nums[cur]) + dfs(mask | 1 << cur, cur) == res) {
                    g(mask | 1 << cur, cur, k + 1);
                    break;
                }
            }
        }
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Solution {
public:
    vector<int> findPermutation(vector<int>& nums) {
        int n = nums.size();
        vector<int> ans;
        int f[1 << n][n];
        memset(f, -1, sizeof(f));
        function<int(int, int)> dfs = [&](int mask, int pre) {
            if (mask == (1 << n) - 1) {
                return abs(pre - nums[0]);
            }
            int* res = &f[mask][pre];
            if (*res != -1) {
                return *res;
            }
            *res = INT_MAX;
            for (int cur = 1; cur < n; ++cur) {
                if (mask >> cur & 1 ^ 1) {
                    *res = min(*res, abs(pre - nums[cur]) + dfs(mask | 1 << cur, cur));
                }
            }
            return *res;
        };
        function<void(int, int)> g = [&](int mask, int pre) {
            ans.push_back(pre);
            if (mask == (1 << n) - 1) {
                return;
            }
            int res = dfs(mask, pre);
            for (int cur = 1; cur < n; ++cur) {
                if (mask >> cur & 1 ^ 1) {
                    if (abs(pre - nums[cur]) + dfs(mask | 1 << cur, cur) == res) {
                        g(mask | 1 << cur, cur);
                        break;
                    }
                }
            }
        };
        g(1, 0);
        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
func findPermutation(nums []int) (ans []int) {
    n := len(nums)
    f := make([][]int, 1<<n)
    for i := range f {
        f[i] = make([]int, n)
        for j := range f[i] {
            f[i][j] = -1
        }
    }
    var dfs func(int, int) int
    dfs = func(mask, pre int) int {
        if mask == 1<<n-1 {
            return abs(pre - nums[0])
        }
        if f[mask][pre] != -1 {
            return f[mask][pre]
        }
        res := &f[mask][pre]
        *res = math.MaxInt32
        for cur := 1; cur < n; cur++ {
            if mask>>cur&1 == 0 {
                *res = min(*res, abs(pre-nums[cur])+dfs(mask|1<<cur, cur))
            }
        }
        return *res
    }
    var g func(int, int)
    g = func(mask, pre int) {
        ans = append(ans, pre)
        if mask == 1<<n-1 {
            return
        }
        res := dfs(mask, pre)
        for cur := 1; cur < n; cur++ {
            if mask>>cur&1 == 0 {
                if abs(pre-nums[cur])+dfs(mask|1<<cur, cur) == res {
                    g(mask|1<<cur, cur)
                    break
                }
            }
        }
    }
    g(1, 0)
    return
}

func abs(x int) int {
    if x < 0 {
        return -x
    }
    return x
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
function findPermutation(nums: number[]): number[] {
    const n = nums.length;
    const ans: number[] = [];
    const f: number[][] = Array.from({ length: 1 << n }, () => Array(n).fill(-1));
    const dfs = (mask: number, pre: number): number => {
        if (mask === (1 << n) - 1) {
            return Math.abs(pre - nums[0]);
        }
        if (f[mask][pre] !== -1) {
            return f[mask][pre];
        }
        let res = Infinity;
        for (let cur = 1; cur < n; ++cur) {
            if (((mask >> cur) & 1) ^ 1) {
                res = Math.min(res, Math.abs(pre - nums[cur]) + dfs(mask | (1 << cur), cur));
            }
        }
        return (f[mask][pre] = res);
    };
    const g = (mask: number, pre: number) => {
        ans.push(pre);
        if (mask === (1 << n) - 1) {
            return;
        }
        const res = dfs(mask, pre);
        for (let cur = 1; cur < n; ++cur) {
            if (((mask >> cur) & 1) ^ 1) {
                if (Math.abs(pre - nums[cur]) + dfs(mask | (1 << cur), cur) === res) {
                    g(mask | (1 << cur), cur);
                    break;
                }
            }
        }
    };
    g(1, 0);
    return ans;
}

Comments