3047. Find the Largest Area of Square Inside Two Rectangles

Description

There exist n rectangles in a 2D plane with edges parallel to the x and y axis. You are given two 2D integer arrays bottomLeft and topRight where bottomLeft[i] = [a_i, b_i] and topRight[i] = [c_i, d_i] represent the bottom-left and top-right coordinates of the i^th rectangle, respectively.

You need to find the maximum area of a square that can fit inside the intersecting region of at least two rectangles. Return 0 if such a square does not exist.

Example 1:

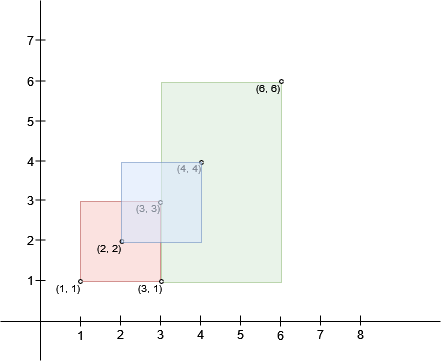
Input: bottomLeft = [[1,1],[2,2],[3,1]], topRight = [[3,3],[4,4],[6,6]]

Output: 1

Explanation:

A square with side length 1 can fit inside either the intersecting region of rectangles 0 and 1 or the intersecting region of rectangles 1 and 2. Hence the maximum area is 1. It can be shown that a square with a greater side length can not fit inside any intersecting region of two rectangles.

Example 2:

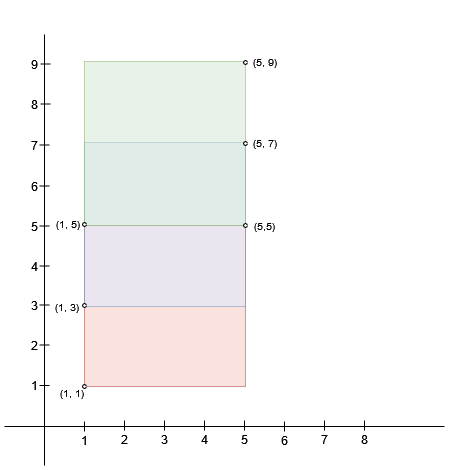
Input: bottomLeft = [[1,1],[1,3],[1,5]], topRight = [[5,5],[5,7],[5,9]]

Output: 4

Explanation:

A square with side length 2 can fit inside either the intersecting region of rectangles 0 and 1 or the intersecting region of rectangles 1 and 2. Hence the maximum area is 2 * 2 = 4. It can be shown that a square with a greater side length can not fit inside any intersecting region of two rectangles.

Example 3:

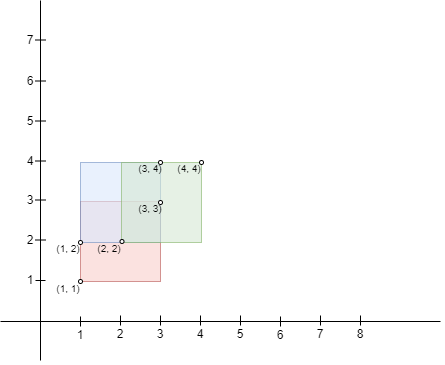
Input: bottomLeft = [[1,1],[2,2],[1,2]], topRight = [[3,3],[4,4],[3,4]]

Output: 1

Explanation:

A square with side length 1 can fit inside the intersecting region of any two rectangles. Also, no larger square can, so the maximum area is 1. Note that the region can be formed by the intersection of more than 2 rectangles.

Example 4:

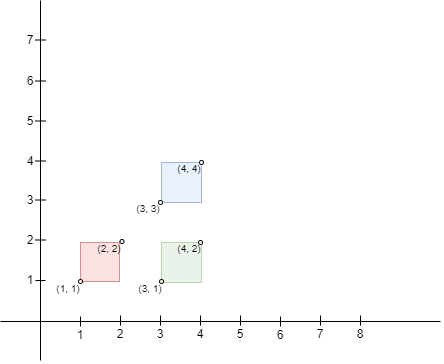
Input: bottomLeft = [[1,1],[3,3],[3,1]], topRight = [[2,2],[4,4],[4,2]]

Output: 0

Explanation:

No pair of rectangles intersect, hence, the answer is 0.

Constraints:

n == bottomLeft.length == topRight.length
2 <= n <= 10³
bottomLeft[i].length == topRight[i].length == 2
1 <= bottomLeft[i][0], bottomLeft[i][1] <= 10⁷
1 <= topRight[i][0], topRight[i][1] <= 10⁷
bottomLeft[i][0] < topRight[i][0]
bottomLeft[i][1] < topRight[i][1]

Solutions

Solution 1: Enumeration

We can enumerate two rectangles, where the coordinates of the bottom left and top right corners of rectangle 1 are $(x_1, y_1)$ and $(x_2, y_2)$ respectively, and the coordinates of the bottom left and top right corners of rectangle 2 are $(x_3, y_3)$ and $(x_4, y_4)$ respectively.

If rectangle 1 and rectangle 2 intersect, then the coordinates of the intersection are:

The x-coordinate of the bottom left corner is the maximum of the x-coordinates of the bottom left corners of the two rectangles, i.e., $\max(x_1, x_3)$;
The y-coordinate of the bottom left corner is the maximum of the y-coordinates of the bottom left corners of the two rectangles, i.e., $\max(y_1, y_3)$;
The x-coordinate of the top right corner is the minimum of the x-coordinates of the top right corners of the two rectangles, i.e., $\min(x_2, x_4)$;
The y-coordinate of the top right corner is the minimum of the y-coordinates of the top right corners of the two rectangles, i.e., $\min(y_2, y_4)$.

Then the width and height of the intersection are $w = \min(x_2, x_4) - \max(x_1, x_3)$ and $h = \min(y_2, y_4) - \max(y_1, y_3)$ respectively. We take the minimum of the two as the side length, i.e., $e = \min(w, h)$. If $e > 0$, then we can get a square with an area of $e^2$. We take the maximum area of all squares.

The time complexity is $O(n^2)$, where $n$ is the number of rectangles. The space complexity is $O(1)$.

Python3JavaC++GoTypeScript

class Solution:
    def largestSquareArea(
        self, bottomLeft: List[List[int]], topRight: List[List[int]]
    ) -> int:
        ans = 0
        for ((x1, y1), (x2, y2)), ((x3, y3), (x4, y4)) in combinations(
            zip(bottomLeft, topRight), 2
        ):
            w = min(x2, x4) - max(x1, x3)
            h = min(y2, y4) - max(y1, y3)
            e = min(w, h)
            if e > 0:
                ans = max(ans, e * e)
        return ans

class Solution {
    public long largestSquareArea(int[][] bottomLeft, int[][] topRight) {
        long ans = 0;
        for (int i = 0; i < bottomLeft.length; ++i) {
            int x1 = bottomLeft[i][0], y1 = bottomLeft[i][1];
            int x2 = topRight[i][0], y2 = topRight[i][1];
            for (int j = i + 1; j < bottomLeft.length; ++j) {
                int x3 = bottomLeft[j][0], y3 = bottomLeft[j][1];
                int x4 = topRight[j][0], y4 = topRight[j][1];
                int w = Math.min(x2, x4) - Math.max(x1, x3);
                int h = Math.min(y2, y4) - Math.max(y1, y3);
                int e = Math.min(w, h);
                if (e > 0) {
                    ans = Math.max(ans, 1L * e * e);
                }
            }
        }
        return ans;
    }
}

class Solution {
public:
    long long largestSquareArea(vector<vector<int>>& bottomLeft, vector<vector<int>>& topRight) {
        long long ans = 0;
        for (int i = 0; i < bottomLeft.size(); ++i) {
            int x1 = bottomLeft[i][0], y1 = bottomLeft[i][1];
            int x2 = topRight[i][0], y2 = topRight[i][1];
            for (int j = i + 1; j < bottomLeft.size(); ++j) {
                int x3 = bottomLeft[j][0], y3 = bottomLeft[j][1];
                int x4 = topRight[j][0], y4 = topRight[j][1];
                int w = min(x2, x4) - max(x1, x3);
                int h = min(y2, y4) - max(y1, y3);
                int e = min(w, h);
                if (e > 0) {
                    ans = max(ans, 1LL * e * e);
                }
            }
        }
        return ans;
    }
};

func largestSquareArea(bottomLeft [][]int, topRight [][]int) (ans int64) {
    for i, b1 := range bottomLeft {
        t1 := topRight[i]
        x1, y1 := b1[0], b1[1]
        x2, y2 := t1[0], t1[1]
        for j := i + 1; j < len(bottomLeft); j++ {
            x3, y3 := bottomLeft[j][0], bottomLeft[j][1]
            x4, y4 := topRight[j][0], topRight[j][1]
            w := min(x2, x4) - max(x1, x3)
            h := min(y2, y4) - max(y1, y3)
            e := min(w, h)
            if e > 0 {
                ans = max(ans, int64(e)*int64(e))
            }
        }
    }
    return
}

function largestSquareArea(bottomLeft: number[][], topRight: number[][]): number {
    let ans = 0;
    for (let i = 0; i < bottomLeft.length; ++i) {
        const [x1, y1] = bottomLeft[i];
        const [x2, y2] = topRight[i];
        for (let j = i + 1; j < bottomLeft.length; ++j) {
            const [x3, y3] = bottomLeft[j];
            const [x4, y4] = topRight[j];
            const w = Math.min(x2, x4) - Math.max(x1, x3);
            const h = Math.min(y2, y4) - Math.max(y1, y3);
            const e = Math.min(w, h);
            if (e > 0) {
                ans = Math.max(ans, e * e);
            }
        }
    }
    return ans;
}

3047. Find the Largest Area of Square Inside Two Rectangles

Description

Solutions

Solution 1: Enumeration

Comments