Skip to content

3025. Find the Number of Ways to Place People I

Description

You are given a 2D array points of size n x 2 representing integer coordinates of some points on a 2D plane, where points[i] = [xi, yi].

Count the number of pairs of points (A, B), where

  • A is on the upper left side of B, and
  • there are no other points in the rectangle (or line) they make (including the border).

Return the count.

 

Example 1:

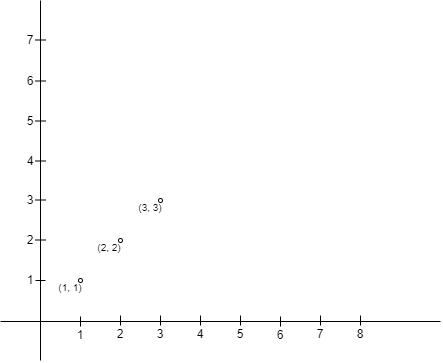
Input: points = [[1,1],[2,2],[3,3]]

Output: 0

Explanation:

There is no way to choose A and B so A is on the upper left side of B.

Example 2:

Input: points = [[6,2],[4,4],[2,6]]

Output: 2

Explanation:

  • The left one is the pair (points[1], points[0]), where points[1] is on the upper left side of points[0] and the rectangle is empty.
  • The middle one is the pair (points[2], points[1]), same as the left one it is a valid pair.
  • The right one is the pair (points[2], points[0]), where points[2] is on the upper left side of points[0], but points[1] is inside the rectangle so it's not a valid pair.

Example 3:

Input: points = [[3,1],[1,3],[1,1]]

Output: 2

Explanation:

  • The left one is the pair (points[2], points[0]), where points[2] is on the upper left side of points[0] and there are no other points on the line they form. Note that it is a valid state when the two points form a line.
  • The middle one is the pair (points[1], points[2]), it is a valid pair same as the left one.
  • The right one is the pair (points[1], points[0]), it is not a valid pair as points[2] is on the border of the rectangle.

 

Constraints:

  • 2 <= n <= 50
  • points[i].length == 2
  • 0 <= points[i][0], points[i][1] <= 50
  • All points[i] are distinct.

Solutions

Solution 1: Sorting and Classification

First, we sort the array. Then, we can classify the results based on the properties of a triangle.

  • If the sum of the two smaller numbers is less than or equal to the largest number, it cannot form a triangle. Return "Invalid".
  • If the three numbers are equal, it is an equilateral triangle. Return "Equilateral".
  • If two numbers are equal, it is an isosceles triangle. Return "Isosceles".
  • If none of the above conditions are met, it is a scalene triangle. Return "Scalene".

The time complexity is $O(1)$, and the space complexity is $O(1)$.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
class Solution:
    def numberOfPairs(self, points: List[List[int]]) -> int:
        points.sort(key=lambda x: (x[0], -x[1]))
        ans = 0
        for i, (_, y1) in enumerate(points):
            max_y = -inf
            for _, y2 in points[i + 1 :]:
                if max_y < y2 <= y1:
                    max_y = y2
                    ans += 1
        return ans

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public int numberOfPairs(int[][] points) {
        Arrays.sort(points, (a, b) -> a[0] == b[0] ? b[1] - a[1] : a[0] - b[0]);
        int ans = 0;
        int n = points.length;
        final int inf = 1 << 30;
        for (int i = 0; i < n; ++i) {
            int y1 = points[i][1];
            int maxY = -inf;
            for (int j = i + 1; j < n; ++j) {
                int y2 = points[j][1];
                if (maxY < y2 && y2 <= y1) {
                    maxY = y2;
                    ++ans;
                }
            }
        }
        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    int numberOfPairs(vector<vector<int>>& points) {
        sort(points.begin(), points.end(), [](const vector<int>& a, const vector<int>& b) {
            return a[0] < b[0] || (a[0] == b[0] && b[1] < a[1]);
        });
        int n = points.size();
        int ans = 0;
        for (int i = 0; i < n; ++i) {
            int y1 = points[i][1];
            int maxY = INT_MIN;
            for (int j = i + 1; j < n; ++j) {
                int y2 = points[j][1];
                if (maxY < y2 && y2 <= y1) {
                    maxY = y2;
                    ++ans;
                }
            }
        }
        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
func numberOfPairs(points [][]int) (ans int) {
    sort.Slice(points, func(i, j int) bool {
        return points[i][0] < points[j][0] || points[i][0] == points[j][0] && points[j][1] < points[i][1]
    })
    for i, p1 := range points {
        y1 := p1[1]
        maxY := math.MinInt32
        for _, p2 := range points[i+1:] {
            y2 := p2[1]
            if maxY < y2 && y2 <= y1 {
                maxY = y2
                ans++
            }
        }
    }
    return
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
function numberOfPairs(points: number[][]): number {
    points.sort((a, b) => (a[0] === b[0] ? b[1] - a[1] : a[0] - b[0]));
    const n = points.length;
    let ans = 0;
    for (let i = 0; i < n; ++i) {
        const [_, y1] = points[i];
        let maxY = -Infinity;
        for (let j = i + 1; j < n; ++j) {
            const [_, y2] = points[j];
            if (maxY < y2 && y2 <= y1) {
                maxY = y2;
                ++ans;
            }
        }
    }
    return ans;
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
public class Solution {
    public int NumberOfPairs(int[][] points) {
        Array.Sort(points, (a, b) => a[0] == b[0] ? b[1] - a[1] : a[0] - b[0]);
        int ans = 0;
        int n = points.Length;
        int inf = 1 << 30;
        for (int i = 0; i < n; ++i) {
            int y1 = points[i][1];
            int maxY = -inf;
            for (int j = i + 1; j < n; ++j) {
                int y2 = points[j][1];
                if (maxY < y2 && y2 <= y1) {
                    maxY = y2;
                    ++ans;
                }
            }
        }
        return ans;
    }
}

Comments