Skip to content

3009. Maximum Number of Intersections on the Chart πŸ”’

Description

There is a line chart consisting of n points connected by line segments. You are given a 1-indexed integer array y. The kth point has coordinates (k, y[k]). There are no horizontal lines; that is, no two consecutive points have the same y-coordinate.

We can draw an infinitely long horizontal line. Return the maximum number of points of intersection of the line with the chart.

 

Example 1:

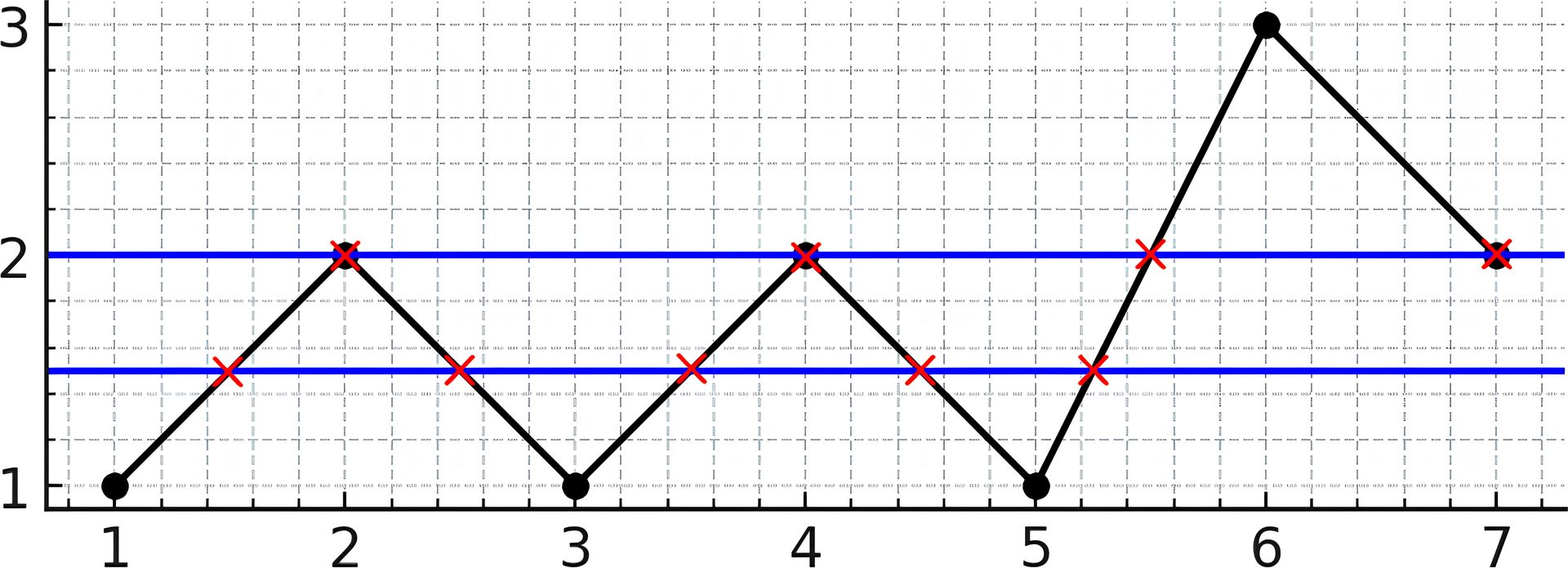
Input: y = [1,2,1,2,1,3,2]
Output: 5
Explanation: As you can see in the image above, the line y = 1.5 has 5 intersections with the chart (in red crosses). You can also see the line y = 2 which intersects the chart in 4 points (in red crosses). It can be shown that there is no horizontal line intersecting the chart at more than 5 points. So the answer would be 5.

Example 2:

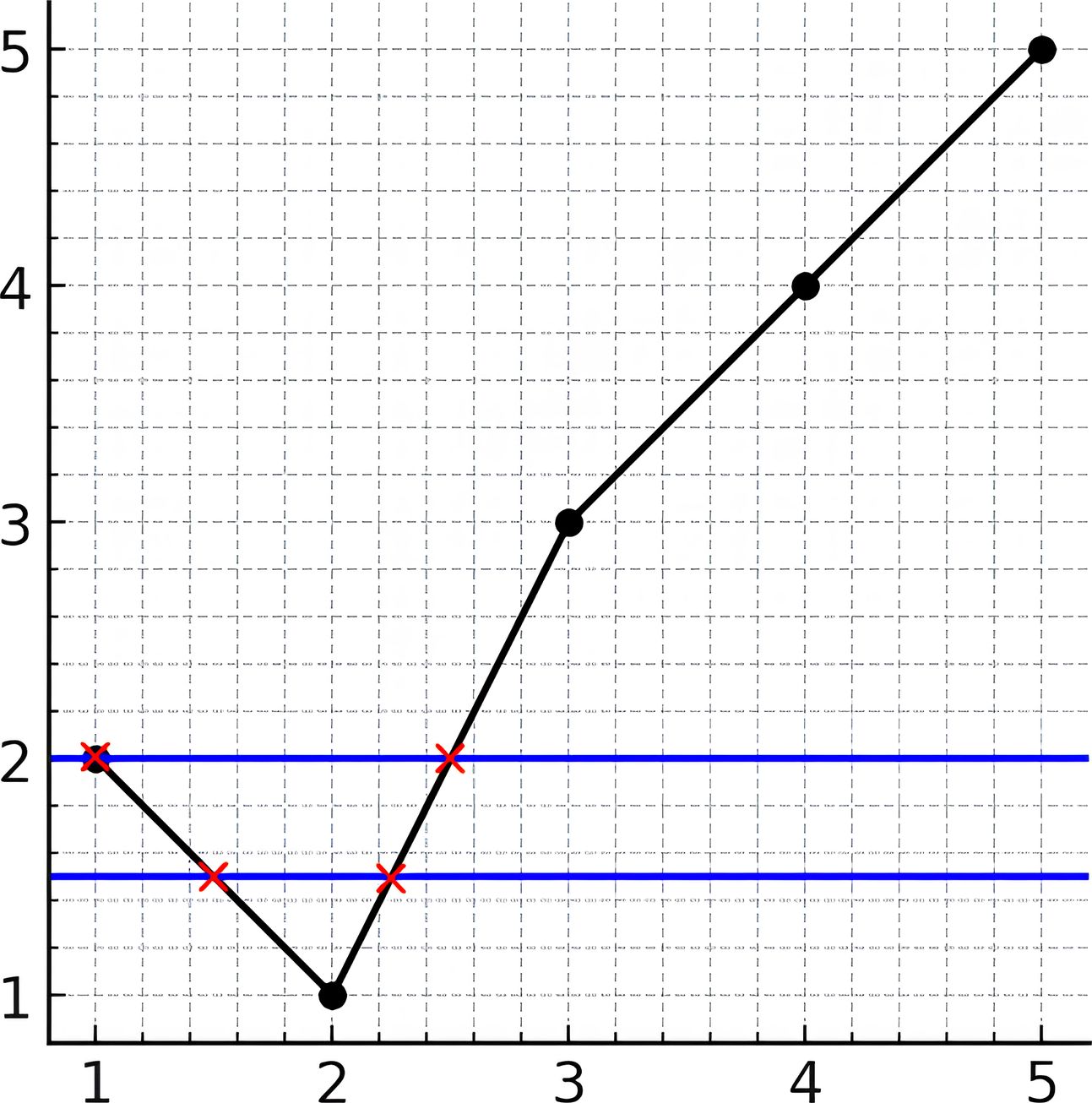
Input: y = [2,1,3,4,5]
Output: 2
Explanation: As you can see in the image above, the line y = 1.5 has 2 intersections with the chart (in red crosses). You can also see the line y = 2 which intersects the chart in 2 points (in red crosses). It can be shown that there is no horizontal line intersecting the chart at more than 2 points. So the answer would be 2.

 

Constraints:

  • 2 <= y.length <= 105
  • 1 <= y[i] <= 109
  • y[i] != y[i + 1] for i in range [1, n - 1]

Solutions

Solution 1

1


 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public int maxIntersectionCount(int[] y) {
        final int n = y.length;
        int ans = 0;
        int intersectionCount = 0;
        TreeMap<Integer, Integer> line = new TreeMap<>();

        for (int i = 1; i < n; ++i) {
            final int start = 2 * y[i - 1];
            final int end = 2 * y[i] + (i == n - 1 ? 0 : y[i] > y[i - 1] ? -1 : 1);
            line.merge(Math.min(start, end), 1, Integer::sum);
            line.merge(Math.max(start, end) + 1, -1, Integer::sum);
        }

        for (final int count : line.values()) {
            intersectionCount += count;
            ans = Math.max(ans, intersectionCount);
        }

        return ans;
    }
}

1


1

Comments