2876. Count Visited Nodes in a Directed Graph

Description

There is a directed graph consisting of n nodes numbered from 0 to n - 1 and n directed edges.

You are given a 0-indexed array edges where edges[i] indicates that there is an edge from node i to node edges[i].

Consider the following process on the graph:

• You start from a node x and keep visiting other nodes through edges until you reach a node that you have already visited before on this same process.

Return an array answer where answer[i] is the number of different nodes that you will visit if you perform the process starting from node i.

 

Example 1:

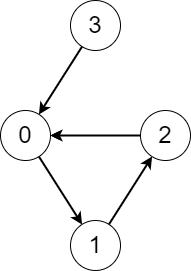
Input: edges = [1,2,0,0]
Output: [3,3,3,4]
Explanation: We perform the process starting from each node in the following way:
- Starting from node 0, we visit the nodes 0 -> 1 -> 2 -> 0. The number of different nodes we visit is 3.
- Starting from node 1, we visit the nodes 1 -> 2 -> 0 -> 1. The number of different nodes we visit is 3.
- Starting from node 2, we visit the nodes 2 -> 0 -> 1 -> 2. The number of different nodes we visit is 3.
- Starting from node 3, we visit the nodes 3 -> 0 -> 1 -> 2 -> 0. The number of different nodes we visit is 4.

Example 2:

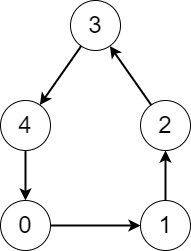
Input: edges = [1,2,3,4,0]
Output: [5,5,5,5,5]
Explanation: Starting from any node we can visit every node in the graph in the process.

 

Constraints:

• n == edges.length
• 2 <= n <= 105
• 0 <= edges[i] <= n - 1
• edges[i] != i

Solutions

Solution 1: Basic Tree + Traversal

We can use an array $ans$ to record the answer for each node, and an array $vis$ to record the visit order for each node.

For each node $i$, if it has not been visited yet, we start traversing from node $i$. There are two cases:

• If we encounter a node that has been visited before during the traversal, then we must have first entered the cycle and then walked around the cycle. For nodes outside the cycle, their answer is the length of the cycle plus the distance from the node to the cycle; for nodes inside the cycle, their answer is the length of the cycle.
• If we encounter a node that has been visited before during the traversal, then for each visited node, its answer is the distance from the current node to this node plus the answer of this node.

The time complexity is $O(n)$, and the space complexity is $O(n)$, where $n$ is the length of the array edges.

Python3JavaC++GoTypeScript

class Solution:
    def countVisitedNodes(self, edges: List[int]) -> List[int]:
        n = len(edges)
        ans = [0] * n
        vis = [0] * n
        for i in range(n):
            if not ans[i]:
                cnt, j = 0, i
                while not vis[j]:
                    cnt += 1
                    vis[j] = cnt
                    j = edges[j]
                cycle, total = 0, cnt + ans[j]
                if not ans[j]:
                    cycle = cnt - vis[j] + 1
                    total = cnt
                j = i
                while not ans[j]:
                    ans[j] = max(total, cycle)
                    total -= 1
                    j = edges[j]
        return ans

class Solution {
    public int[] countVisitedNodes(List<Integer> edges) {
        int n = edges.size();
        int[] ans = new int[n];
        int[] vis = new int[n];
        for (int i = 0; i < n; ++i) {
            if (ans[i] == 0) {
                int cnt = 0, j = i;
                while (vis[j] == 0) {
                    vis[j] = ++cnt;
                    j = edges.get(j);
                }
                int cycle = 0, total = cnt + ans[j];
                if (ans[j] == 0) {
                    cycle = cnt - vis[j] + 1;
                }
                j = i;
                while (ans[j] == 0) {
                    ans[j] = Math.max(total--, cycle);
                    j = edges.get(j);
                }
            }
        }
        return ans;
    }
}

class Solution {
public:
    vector<int> countVisitedNodes(vector<int>& edges) {
        int n = edges.size();
        vector<int> ans(n), vis(n);
        for (int i = 0; i < n; ++i) {
            if (!ans[i]) {
                int cnt = 0, j = i;
                while (vis[j] == 0) {
                    vis[j] = ++cnt;
                    j = edges[j];
                }
                int cycle = 0, total = cnt + ans[j];
                if (ans[j] == 0) {
                    cycle = cnt - vis[j] + 1;
                }
                j = i;
                while (ans[j] == 0) {
                    ans[j] = max(total--, cycle);
                    j = edges[j];
                }
            }
        }
        return ans;
    }
};

func countVisitedNodes(edges []int) []int {
    n := len(edges)
    ans := make([]int, n)
    vis := make([]int, n)
    for i := range ans {
        if ans[i] == 0 {
            cnt, j := 0, i
            for vis[j] == 0 {
                cnt++
                vis[j] = cnt
                j = edges[j]
            }
            cycle, total := 0, cnt+ans[j]
            if ans[j] == 0 {
                cycle = cnt - vis[j] + 1
            }
            j = i
            for ans[j] == 0 {
                ans[j] = max(total, cycle)
                total--
                j = edges[j]
            }
        }
    }
    return ans
}

function countVisitedNodes(edges: number[]): number[] {
    const n = edges.length;
    const ans: number[] = Array(n).fill(0);
    const vis: number[] = Array(n).fill(0);
    for (let i = 0; i < n; ++i) {
        if (ans[i] === 0) {
            let [cnt, j] = [0, i];
            while (vis[j] === 0) {
                vis[j] = ++cnt;
                j = edges[j];
            }
            let [cycle, total] = [0, cnt + ans[j]];
            if (ans[j] === 0) {
                cycle = cnt - vis[j] + 1;
            }
            j = i;
            while (ans[j] === 0) {
                ans[j] = Math.max(total--, cycle);
                j = edges[j];
            }
        }
    }
    return ans;
}

Comments