2858. Minimum Edge Reversals So Every Node Is Reachable

Description

There is a simple directed graph with n nodes labeled from 0 to n - 1. The graph would form a tree if its edges were bi-directional.

You are given an integer n and a 2D integer array edges, where edges[i] = [ui, vi] represents a directed edge going from node ui to node vi.

An edge reversal changes the direction of an edge, i.e., a directed edge going from node ui to node vi becomes a directed edge going from node vi to node ui.

For every node i in the range [0, n - 1], your task is to independently calculate the minimum number of edge reversals required so it is possible to reach any other node starting from node i through a sequence of directed edges.

Return an integer array answer, where answer[i] is the minimum number of edge reversals required so it is possible to reach any other node starting from node i through a sequence of directed edges.

 

Example 1:

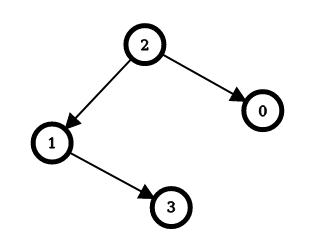
Input: n = 4, edges = [[2,0],[2,1],[1,3]]
Output: [1,1,0,2]
Explanation: The image above shows the graph formed by the edges.
For node 0: after reversing the edge [2,0], it is possible to reach any other node starting from node 0.
So, answer[0] = 1.
For node 1: after reversing the edge [2,1], it is possible to reach any other node starting from node 1.
So, answer[1] = 1.
For node 2: it is already possible to reach any other node starting from node 2.
So, answer[2] = 0.
For node 3: after reversing the edges [1,3] and [2,1], it is possible to reach any other node starting from node 3.
So, answer[3] = 2.

Example 2:

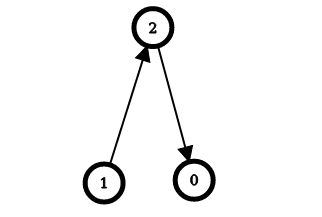
Input: n = 3, edges = [[1,2],[2,0]]
Output: [2,0,1]
Explanation: The image above shows the graph formed by the edges.
For node 0: after reversing the edges [2,0] and [1,2], it is possible to reach any other node starting from node 0.
So, answer[0] = 2.
For node 1: it is already possible to reach any other node starting from node 1.
So, answer[1] = 0.
For node 2: after reversing the edge [1, 2], it is possible to reach any other node starting from node 2.
So, answer[2] = 1.

 

Constraints:

• 2 <= n <= 105
• edges.length == n - 1
• edges[i].length == 2
• 0 <= ui == edges[i][0] < n
• 0 <= vi == edges[i][1] < n
• ui != vi
• The input is generated such that if the edges were bi-directional, the graph would be a tree.

Solutions

Solution 1

Python3JavaC++GoTypeScript

class Solution:
    def minEdgeReversals(self, n: int, edges: List[List[int]]) -> List[int]:
        ans = [0] * n
        g = [[] for _ in range(n)]
        for x, y in edges:
            g[x].append((y, 1))
            g[y].append((x, -1))

        def dfs(i: int, fa: int):
            for j, k in g[i]:
                if j != fa:
                    ans[0] += int(k < 0)
                    dfs(j, i)

        dfs(0, -1)

        def dfs2(i: int, fa: int):
            for j, k in g[i]:
                if j != fa:
                    ans[j] = ans[i] + k
                    dfs2(j, i)

        dfs2(0, -1)
        return ans

class Solution {
    private List<int[]>[] g;
    private int[] ans;

    public int[] minEdgeReversals(int n, int[][] edges) {
        ans = new int[n];
        g = new List[n];
        Arrays.setAll(g, i -> new ArrayList<>());
        for (var e : edges) {
            int x = e[0], y = e[1];
            g[x].add(new int[] {y, 1});
            g[y].add(new int[] {x, -1});
        }
        dfs(0, -1);
        dfs2(0, -1);
        return ans;
    }

    private void dfs(int i, int fa) {
        for (var ne : g[i]) {
            int j = ne[0], k = ne[1];
            if (j != fa) {
                ans[0] += k < 0 ? 1 : 0;
                dfs(j, i);
            }
        }
    }

    private void dfs2(int i, int fa) {
        for (var ne : g[i]) {
            int j = ne[0], k = ne[1];
            if (j != fa) {
                ans[j] = ans[i] + k;
                dfs2(j, i);
            }
        }
    }
}

class Solution {
public:
    vector<int> minEdgeReversals(int n, vector<vector<int>>& edges) {
        vector<pair<int, int>> g[n];
        vector<int> ans(n);
        for (auto& e : edges) {
            int x = e[0], y = e[1];
            g[x].emplace_back(y, 1);
            g[y].emplace_back(x, -1);
        }
        function<void(int, int)> dfs = [&](int i, int fa) {
            for (auto& [j, k] : g[i]) {
                if (j != fa) {
                    ans[0] += k < 0;
                    dfs(j, i);
                }
            }
        };
        function<void(int, int)> dfs2 = [&](int i, int fa) {
            for (auto& [j, k] : g[i]) {
                if (j != fa) {
                    ans[j] = ans[i] + k;
                    dfs2(j, i);
                }
            }
        };
        dfs(0, -1);
        dfs2(0, -1);
        return ans;
    }
};

func minEdgeReversals(n int, edges [][]int) []int {
    g := make([][][2]int, n)
    for _, e := range edges {
        x, y := e[0], e[1]
        g[x] = append(g[x], [2]int{y, 1})
        g[y] = append(g[y], [2]int{x, -1})
    }
    ans := make([]int, n)
    var dfs func(int, int)
    var dfs2 func(int, int)
    dfs = func(i, fa int) {
        for _, ne := range g[i] {
            j, k := ne[0], ne[1]
            if j != fa {
                if k < 0 {
                    ans[0]++
                }
                dfs(j, i)
            }
        }
    }
    dfs2 = func(i, fa int) {
        for _, ne := range g[i] {
            j, k := ne[0], ne[1]
            if j != fa {
                ans[j] = ans[i] + k
                dfs2(j, i)
            }
        }
    }
    dfs(0, -1)
    dfs2(0, -1)
    return ans
}

function minEdgeReversals(n: number, edges: number[][]): number[] {
    const g: number[][][] = Array.from({ length: n }, () => []);
    for (const [x, y] of edges) {
        g[x].push([y, 1]);
        g[y].push([x, -1]);
    }
    const ans: number[] = Array(n).fill(0);
    const dfs = (i: number, fa: number) => {
        for (const [j, k] of g[i]) {
            if (j !== fa) {
                ans[0] += k < 0 ? 1 : 0;
                dfs(j, i);
            }
        }
    };
    const dfs2 = (i: number, fa: number) => {
        for (const [j, k] of g[i]) {
            if (j !== fa) {
                ans[j] = ans[i] + k;
                dfs2(j, i);
            }
        }
    };
    dfs(0, -1);
    dfs2(0, -1);
    return ans;
}

Comments