2852. Sum of Remoteness of All Cells 🔒

Description

You are given a 0-indexed matrix grid of order n * n. Each cell in this matrix has a value grid[i][j], which is either a positive integer or -1 representing a blocked cell.

You can move from a non-blocked cell to any non-blocked cell that shares an edge.

For any cell (i, j), we represent its remoteness as R[i][j] which is defined as the following:

• If the cell (i, j) is a non-blocked cell, R[i][j] is the sum of the values grid[x][y] such that there is no path from the non-blocked cell (x, y) to the cell (i, j).
• For blocked cells, R[i][j] == 0.

Return the sum of R[i][j] over all cells.

 

Example 1:

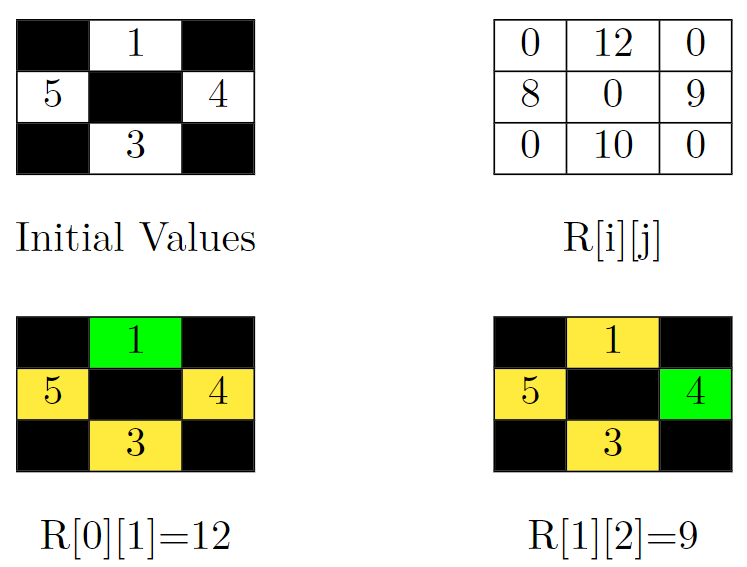
Input: grid = [[-1,1,-1],[5,-1,4],[-1,3,-1]]
Output: 39
Explanation: In the picture above, there are four grids. The top-left grid contains the initial values in the grid. Blocked cells are colored black, and other cells get their values as it is in the input. In the top-right grid, you can see the value of R[i][j] for all cells. So the answer would be the sum of them. That is: 0 + 12 + 0 + 8 + 0 + 9 + 0 + 10 + 0 = 39.
Let's jump on the bottom-left grid in the above picture and calculate R[0][1] (the target cell is colored green). We should sum up the value of cells that can't be reached by the cell (0, 1). These cells are colored yellow in this grid. So R[0][1] = 5 + 4 + 3 = 12.
Now let's jump on the bottom-right grid in the above picture and calculate R[1][2] (the target cell is colored green). We should sum up the value of cells that can't be reached by the cell (1, 2). These cells are colored yellow in this grid. So R[1][2] = 1 + 5 + 3 = 9.

Example 2:

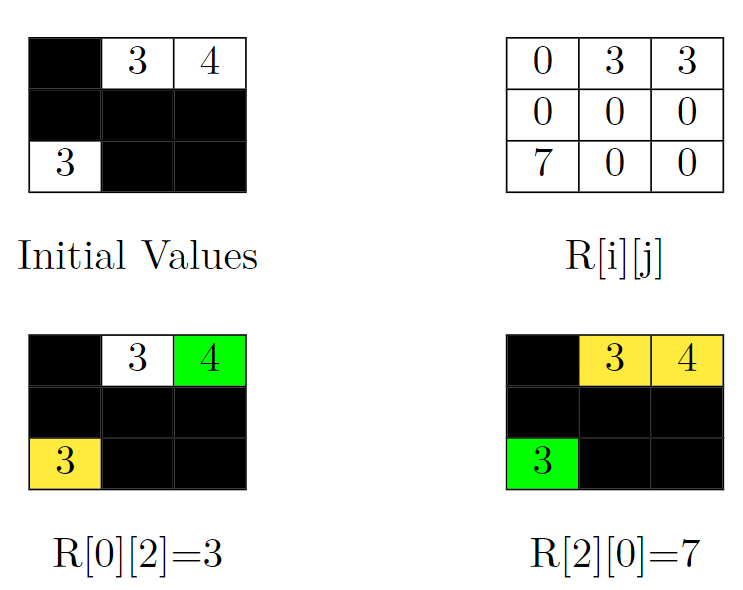
Input: grid = [[-1,3,4],[-1,-1,-1],[3,-1,-1]]
Output: 13
Explanation: In the picture above, there are four grids. The top-left grid contains the initial values in the grid. Blocked cells are colored black, and other cells get their values as it is in the input. In the top-right grid, you can see the value of R[i][j] for all cells. So the answer would be the sum of them. That is: 3 + 3 + 0 + 0 + 0 + 0 + 7 + 0 + 0 = 13.
Let's jump on the bottom-left grid in the above picture and calculate R[0][2] (the target cell is colored green). We should sum up the value of cells that can't be reached by the cell (0, 2). This cell is colored yellow in this grid. So R[0][2] = 3.
Now let's jump on the bottom-right grid in the above picture and calculate R[2][0] (the target cell is colored green). We should sum up the value of cells that can't be reached by the cell (2, 0). These cells are colored yellow in this grid. So R[2][0] = 3 + 4 = 7.

Example 3:

Input: grid = [[1]]
Output: 0
Explanation: Since there are no other cells than (0, 0), R[0][0] is equal to 0. So the sum of R[i][j] over all cells would be 0.

 

Constraints:

• 1 <= n <= 300
• 1 <= grid[i][j] <= 106 or grid[i][j] == -1

Solutions

Solution 1: DFS

First, we count the number of non-blocking cells in the matrix, denoted as $cnt$. Then, starting from each non-blocking cell, we use DFS to calculate the sum $s$ of the cells in each connected block and the number of cells $t$. Then, all $(cnt - t)$ cells in other connected blocks can be added with $s$. We sum up the results of all connected blocks.

The time complexity is $O(n^2)$, and the space complexity is $O(n^2)$. Here, $n$ is the side length of the matrix.

Python3JavaC++GoTypeScript

class Solution:
    def sumRemoteness(self, grid: List[List[int]]) -> int:
        def dfs(i: int, j: int) -> (int, int):
            s, t = grid[i][j], 1
            grid[i][j] = 0
            for a, b in pairwise(dirs):
                x, y = i + a, j + b
                if 0 <= x < n and 0 <= y < n and grid[x][y] > 0:
                    s1, t1 = dfs(x, y)
                    s, t = s + s1, t + t1
            return s, t

        n = len(grid)
        dirs = (-1, 0, 1, 0, -1)
        cnt = sum(x > 0 for row in grid for x in row)
        ans = 0
        for i, row in enumerate(grid):
            for j, x in enumerate(row):
                if x > 0:
                    s, t = dfs(i, j)
                    ans += (cnt - t) * s
        return ans

class Solution {
    private int n;
    private int[][] grid;
    private final int[] dirs = {-1, 0, 1, 0, -1};

    public long sumRemoteness(int[][] grid) {
        n = grid.length;
        this.grid = grid;
        int cnt = 0;
        for (int[] row : grid) {
            for (int x : row) {
                if (x > 0) {
                    ++cnt;
                }
            }
        }
        long ans = 0;
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] > 0) {
                    long[] res = dfs(i, j);
                    ans += (cnt - res[1]) * res[0];
                }
            }
        }
        return ans;
    }

    private long[] dfs(int i, int j) {
        long[] res = new long[2];
        res[0] = grid[i][j];
        res[1] = 1;
        grid[i][j] = 0;
        for (int k = 0; k < 4; ++k) {
            int x = i + dirs[k], y = j + dirs[k + 1];
            if (x >= 0 && x < n && y >= 0 && y < n && grid[x][y] > 0) {
                long[] tmp = dfs(x, y);
                res[0] += tmp[0];
                res[1] += tmp[1];
            }
        }
        return res;
    }
}

class Solution {
public:
    long long sumRemoteness(vector<vector<int>>& grid) {
        using pli = pair<long long, int>;
        int n = grid.size();
        int cnt = 0;
        for (auto& row : grid) {
            for (int x : row) {
                cnt += x > 0;
            }
        }
        int dirs[5] = {-1, 0, 1, 0, -1};
        function<pli(int, int)> dfs = [&](int i, int j) {
            long long s = grid[i][j];
            int t = 1;
            grid[i][j] = 0;
            for (int k = 0; k < 4; ++k) {
                int x = i + dirs[k], y = j + dirs[k + 1];
                if (x >= 0 && x < n && y >= 0 && y < n && grid[x][y] > 0) {
                    auto [ss, tt] = dfs(x, y);
                    s += ss;
                    t += tt;
                }
            }
            return pli(s, t);
        };
        long long ans = 0;
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] > 0) {
                    auto [s, t] = dfs(i, j);
                    ans += (cnt - t) * s;
                }
            }
        }
        return ans;
    }
};

func sumRemoteness(grid [][]int) (ans int64) {
    n := len(grid)
    cnt := 0
    for _, row := range grid {
        for _, x := range row {
            if x > 0 {
                cnt++
            }
        }
    }
    var dfs func(i, j int) (int, int)
    dfs = func(i, j int) (int, int) {
        s, t := grid[i][j], 1
        grid[i][j] = 0
        dirs := [5]int{-1, 0, 1, 0, -1}
        for k := 0; k < 4; k++ {
            x, y := i+dirs[k], j+dirs[k+1]
            if x >= 0 && x < n && y >= 0 && y < n && grid[x][y] > 0 {
                ss, tt := dfs(x, y)
                s += ss
                t += tt
            }
        }
        return s, t
    }
    for i := range grid {
        for j := range grid[i] {
            if grid[i][j] > 0 {
                s, t := dfs(i, j)
                ans += int64(cnt-t) * int64(s)
            }
        }
    }
    return
}

function sumRemoteness(grid: number[][]): number {
    const n = grid.length;
    let cnt = 0;
    for (const row of grid) {
        for (const x of row) {
            if (x > 0) {
                cnt++;
            }
        }
    }
    const dirs = [-1, 0, 1, 0, -1];
    const dfs = (i: number, j: number): [number, number] => {
        let s = grid[i][j];
        let t = 1;
        grid[i][j] = 0;
        for (let k = 0; k < 4; ++k) {
            const [x, y] = [i + dirs[k], j + dirs[k + 1]];
            if (x >= 0 && x < n && y >= 0 && y < n && grid[x][y] > 0) {
                const [ss, tt] = dfs(x, y);
                s += ss;
                t += tt;
            }
        }
        return [s, t];
    };
    let ans = 0;
    for (let i = 0; i < n; ++i) {
        for (let j = 0; j < n; ++j) {
            if (grid[i][j] > 0) {
                const [s, t] = dfs(i, j);
                ans += (cnt - t) * s;
            }
        }
    }
    return ans;
}

Comments