276. Paint Fence 🔒

Description

You are painting a fence of n posts with k different colors. You must paint the posts following these rules:

• Every post must be painted exactly one color.
• There cannot be three or more consecutive posts with the same color.

Given the two integers n and k, return the number of ways you can paint the fence.

 

Example 1:

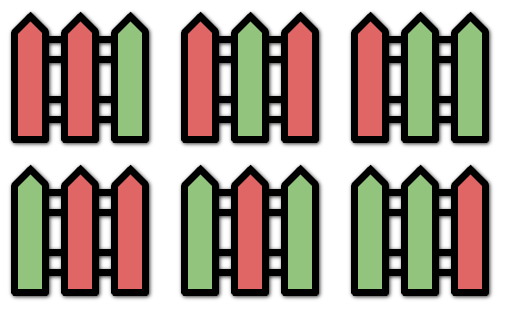
Input: n = 3, k = 2
Output: 6
Explanation: All the possibilities are shown.
Note that painting all the posts red or all the posts green is invalid because there cannot be three posts in a row with the same color.

Example 2:

Input: n = 1, k = 1
Output: 1

Example 3:

Input: n = 7, k = 2
Output: 42

 

Constraints:

• 1 <= n <= 50
• 1 <= k <= 105
• The testcases are generated such that the answer is in the range [0, 231 - 1] for the given n and k.

Solutions

Solution 1: Dynamic Programming

We define \(f[i]\) to represent the number of ways to paint the fence posts from \([0..i]\) such that the last two posts have different colors, and \(g[i]\) to represent the number of ways to paint the fence posts from \([0..i]\) such that the last two posts have the same color. Initially, \(f[0] = k\) and \(g[0] = 0\).

When \(i > 0\), we have the following state transition equations:

\[ \begin{aligned} f[i] & = (f[i - 1] + g[i - 1]) \times (k - 1) \\ g[i] & = f[i - 1] \end{aligned} \]

The final answer is \(f[n - 1] + g[n - 1]\).

The time complexity is \(O(n)\) and the space complexity is \(O(n)\), where \(n\) is the number of fence posts.

Python3JavaC++GoTypeScript

class Solution:
    def numWays(self, n: int, k: int) -> int:
        f = [0] * n
        g = [0] * n
        f[0] = k
        for i in range(1, n):
            f[i] = (f[i - 1] + g[i - 1]) * (k - 1)
            g[i] = f[i - 1]
        return f[-1] + g[-1]

class Solution {
    public int numWays(int n, int k) {
        int[] f = new int[n];
        int[] g = new int[n];
        f[0] = k;
        for (int i = 1; i < n; ++i) {
            f[i] = (f[i - 1] + g[i - 1]) * (k - 1);
            g[i] = f[i - 1];
        }
        return f[n - 1] + g[n - 1];
    }
}

class Solution {
public:
    int numWays(int n, int k) {
        vector<int> f(n);
        vector<int> g(n);
        f[0] = k;
        for (int i = 1; i < n; ++i) {
            f[i] = (f[i - 1] + g[i - 1]) * (k - 1);
            g[i] = f[i - 1];
        }
        return f[n - 1] + g[n - 1];
    }
};

func numWays(n int, k int) int {
    f := make([]int, n)
    g := make([]int, n)
    f[0] = k
    for i := 1; i < n; i++ {
        f[i] = (f[i-1] + g[i-1]) * (k - 1)
        g[i] = f[i-1]
    }
    return f[n-1] + g[n-1]
}

function numWays(n: number, k: number): number {
    const f: number[] = Array(n).fill(0);
    const g: number[] = Array(n).fill(0);
    f[0] = k;
    for (let i = 1; i < n; ++i) {
        f[i] = (f[i - 1] + g[i - 1]) * (k - 1);
        g[i] = f[i - 1];
    }
    return f[n - 1] + g[n - 1];
}

Solution 2: Dynamic Programming (Space Optimization)

We notice that \(f[i]\) and \(g[i]\) are only related to \(f[i - 1]\) and \(g[i - 1]\). Therefore, we can use two variables \(f\) and \(g\) to record the values of \(f[i - 1]\) and \(g[i - 1]\) respectively, thus optimizing the space complexity to \(O(1)\).

Python3JavaC++GoTypeScript

class Solution:
    def numWays(self, n: int, k: int) -> int:
        f, g = k, 0
        for _ in range(n - 1):
            ff = (f + g) * (k - 1)
            g = f
            f = ff
        return f + g

class Solution {
    public int numWays(int n, int k) {
        int f = k, g = 0;
        for (int i = 1; i < n; ++i) {
            int ff = (f + g) * (k - 1);
            g = f;
            f = ff;
        }
        return f + g;
    }
}

class Solution {
public:
    int numWays(int n, int k) {
        int f = k, g = 0;
        for (int i = 1; i < n; ++i) {
            int ff = (f + g) * (k - 1);
            g = f;
            f = ff;
        }
        return f + g;
    }
};

func numWays(n int, k int) int {
    f, g := k, 0
    for i := 1; i < n; i++ {
        f, g = (f+g)*(k-1), f
    }
    return f + g
}

function numWays(n: number, k: number): number {
    let [f, g] = [k, 0];
    for (let i = 1; i < n; ++i) {
        const ff = (f + g) * (k - 1);
        g = f;
        f = ff;
    }
    return f + g;
}

Comments