Binary Search Tree
Binary Tree
Depth-First Search
Heap (Priority Queue)
Stack
Tree
Two Pointers
Description
Given the root of a binary search tree, a target value, and an integer k, return the k values in the BST that are closest to the target. You may return the answer in any order .
You are guaranteed to have only one unique set of k values in the BST that are closest to the target.
Example 1:
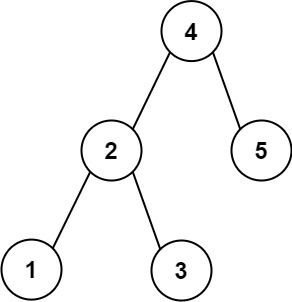
Input: root = [4,2,5,1,3], target = 3.714286, k = 2
Output: [4,3]
Example 2:
Input: root = [1], target = 0.000000, k = 1
Output: [1]
Constraints:
The number of nodes in the tree is n.
1 <= k <= n <= 104 .0 <= Node.val <= 109 -109 <= target <= 109
Follow up: Assume that the BST is balanced. Could you solve it in less than O(n) runtime (where n = total nodes)?
Solutions
Solution 1
Python3 Java C++ Go
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24 # Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution :
def closestKValues ( self , root : TreeNode , target : float , k : int ) -> List [ int ]:
def dfs ( root ):
if root is None :
return
dfs ( root . left )
if len ( q ) < k :
q . append ( root . val )
else :
if abs ( root . val - target ) >= abs ( q [ 0 ] - target ):
return
q . popleft ()
q . append ( root . val )
dfs ( root . right )
q = deque ()
dfs ( root )
return list ( q )
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46 /**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
private List < Integer > ans ;
private double target ;
private int k ;
public List < Integer > closestKValues ( TreeNode root , double target , int k ) {
ans = new LinkedList <> ();
this . target = target ;
this . k = k ;
dfs ( root );
return ans ;
}
private void dfs ( TreeNode root ) {
if ( root == null ) {
return ;
}
dfs ( root . left );
if ( ans . size () < k ) {
ans . add ( root . val );
} else {
if ( Math . abs ( root . val - target ) >= Math . abs ( ans . get ( 0 ) - target )) {
return ;
}
ans . remove ( 0 );
ans . add ( root . val );
}
dfs ( root . right );
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42 /**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public :
queue < int > q ;
double target ;
int k ;
vector < int > closestKValues ( TreeNode * root , double target , int k ) {
this -> target = target ;
this -> k = k ;
dfs ( root );
vector < int > ans ;
while ( ! q . empty ()) {
ans . push_back ( q . front ());
q . pop ();
}
return ans ;
}
void dfs ( TreeNode * root ) {
if ( ! root ) return ;
dfs ( root -> left );
if ( q . size () < k )
q . push ( root -> val );
else {
if ( abs ( root -> val - target ) >= abs ( q . front () - target )) return ;
q . pop ();
q . push ( root -> val );
}
dfs ( root -> right );
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30 /**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func closestKValues ( root * TreeNode , target float64 , k int ) [] int {
var ans [] int
var dfs func ( root * TreeNode )
dfs = func ( root * TreeNode ) {
if root == nil {
return
}
dfs ( root . Left )
if len ( ans ) < k {
ans = append ( ans , root . Val )
} else {
if math . Abs ( float64 ( root . Val ) - target ) >= math . Abs ( float64 ( ans [ 0 ]) - target ) {
return
}
ans = ans [ 1 :]
ans = append ( ans , root . Val )
}
dfs ( root . Right )
}
dfs ( root )
return ans
}
GitHub