2718. Sum of Matrix After Queries

Description

You are given an integer n and a 0-indexed 2D array queries where queries[i] = [typei, indexi, vali].

Initially, there is a 0-indexed n x n matrix filled with 0's. For each query, you must apply one of the following changes:

• if typei == 0, set the values in the row with indexi to vali, overwriting any previous values.
• if typei == 1, set the values in the column with indexi to vali, overwriting any previous values.

Return the sum of integers in the matrix after all queries are applied.

 

Example 1:

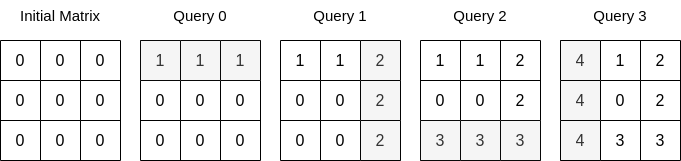
Input: n = 3, queries = [[0,0,1],[1,2,2],[0,2,3],[1,0,4]]
Output: 23
Explanation: The image above describes the matrix after each query. The sum of the matrix after all queries are applied is 23. 

Example 2:

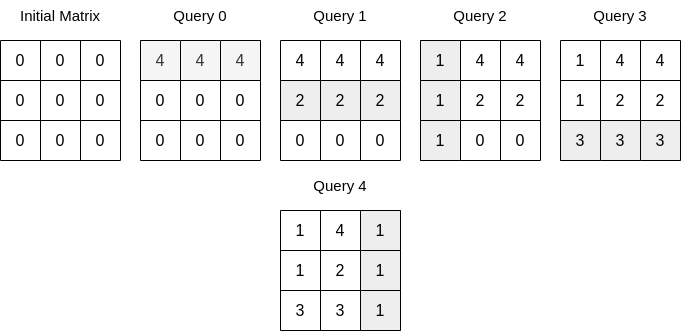
Input: n = 3, queries = [[0,0,4],[0,1,2],[1,0,1],[0,2,3],[1,2,1]]
Output: 17
Explanation: The image above describes the matrix after each query. The sum of the matrix after all queries are applied is 17.

 

Constraints:

• 1 <= n <= 104
• 1 <= queries.length <= 5 * 104
• queries[i].length == 3
• 0 <= typei <= 1
• 0 <= indexi < n
• 0 <= vali <= 105

Solutions

Solution 1: Hash Table

Since the value of each row and column depends on the last modification, we can traverse all queries in reverse order and use hash tables $row$ and $col$ to record which rows and columns have been modified.

For each query $(t, i, v)$:

• If $t = 0$, we check whether the $i$th row has been modified. If not, we add $v \times (n - |col|)$ to the answer, where $|col|$ represents the size of $col$, and then add $i$ to $row$.
• If $t = 1$, we check whether the $i$th column has been modified. If not, we add $v \times (n - |row|)$ to the answer, where $|row|$ represents the size of $row$, and then add $i$ to $col$.

Finally, return the answer.

The time complexity is $O(m)$, and the space complexity is $O(n)$. Here, $m$ represents the number of queries.

Python3JavaC++GoTypeScript

class Solution:
    def matrixSumQueries(self, n: int, queries: List[List[int]]) -> int:
        row = set()
        col = set()
        ans = 0
        for t, i, v in queries[::-1]:
            if t == 0:
                if i not in row:
                    ans += v * (n - len(col))
                    row.add(i)
            else:
                if i not in col:
                    ans += v * (n - len(row))
                    col.add(i)
        return ans

class Solution {
    public long matrixSumQueries(int n, int[][] queries) {
        Set<Integer> row = new HashSet<>();
        Set<Integer> col = new HashSet<>();
        int m = queries.length;
        long ans = 0;
        for (int k = m - 1; k >= 0; --k) {
            var q = queries[k];
            int t = q[0], i = q[1], v = q[2];
            if (t == 0) {
                if (row.add(i)) {
                    ans += 1L * (n - col.size()) * v;
                }
            } else {
                if (col.add(i)) {
                    ans += 1L * (n - row.size()) * v;
                }
            }
        }
        return ans;
    }
}

class Solution {
public:
    long long matrixSumQueries(int n, vector<vector<int>>& queries) {
        unordered_set<int> row, col;
        reverse(queries.begin(), queries.end());
        long long ans = 0;
        for (auto& q : queries) {
            int t = q[0], i = q[1], v = q[2];
            if (t == 0) {
                if (!row.count(i)) {
                    ans += 1LL * (n - col.size()) * v;
                    row.insert(i);
                }
            } else {
                if (!col.count(i)) {
                    ans += 1LL * (n - row.size()) * v;
                    col.insert(i);
                }
            }
        }
        return ans;
    }
};

func matrixSumQueries(n int, queries [][]int) (ans int64) {
    row, col := map[int]bool{}, map[int]bool{}
    m := len(queries)
    for k := m - 1; k >= 0; k-- {
        t, i, v := queries[k][0], queries[k][1], queries[k][2]
        if t == 0 {
            if !row[i] {
                ans += int64(v * (n - len(col)))
                row[i] = true
            }
        } else {
            if !col[i] {
                ans += int64(v * (n - len(row)))
                col[i] = true
            }
        }
    }
    return
}

function matrixSumQueries(n: number, queries: number[][]): number {
    const row: Set<number> = new Set();
    const col: Set<number> = new Set();
    let ans = 0;
    queries.reverse();
    for (const [t, i, v] of queries) {
        if (t === 0) {
            if (!row.has(i)) {
                ans += v * (n - col.size);
                row.add(i);
            }
        } else {
            if (!col.has(i)) {
                ans += v * (n - row.size);
                col.add(i);
            }
        }
    }
    return ans;
}

Comments