2556. Disconnect Path in a Binary Matrix by at Most One Flip

Description

You are given a 0-indexed m x n binary matrix grid. You can move from a cell (row, col) to any of the cells (row + 1, col) or (row, col + 1) that has the value 1. The matrix is disconnected if there is no path from (0, 0) to (m - 1, n - 1).

You can flip the value of at most one (possibly none) cell. You cannot flip the cells (0, 0) and (m - 1, n - 1).

Return true if it is possible to make the matrix disconnect or false otherwise.

Note that flipping a cell changes its value from 0 to 1 or from 1 to 0.

Example 1:

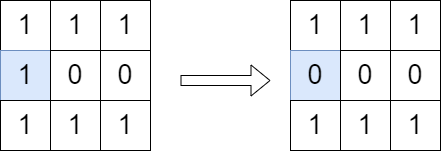
Input: grid = [[1,1,1],[1,0,0],[1,1,1]]
Output: true
Explanation: We can change the cell shown in the diagram above. There is no path from (0, 0) to (2, 2) in the resulting grid.

Example 2:

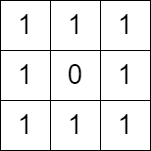
Input: grid = [[1,1,1],[1,0,1],[1,1,1]]
Output: false
Explanation: It is not possible to change at most one cell such that there is not path from (0, 0) to (2, 2).

Constraints:

m == grid.length
n == grid[i].length
1 <= m, n <= 1000
1 <= m * n <= 10⁵
grid[i][j] is either 0 or 1.
grid[0][0] == grid[m - 1][n - 1] == 1

Solutions

Solution 1: Two DFS Traversals

First, we perform a DFS traversal to determine whether there is a path from \((0, 0)\) to \((m - 1, n - 1)\), and we denote the result as \(a\). During the DFS process, we set the value of the visited cells to \(0\) to prevent revisiting.

Next, we set the values of \((0, 0)\) and \((m - 1, n - 1)\) to \(1\), and perform another DFS traversal to determine whether there is a path from \((0, 0)\) to \((m - 1, n - 1)\), and we denote the result as \(b\). During the DFS process, we set the value of the visited cells to \(0\) to avoid revisiting.

Finally, if both \(a\) and \(b\) are true, we return false, otherwise, we return true.

The time complexity is \(O(m \times n)\), and the space complexity is \(O(m \times n)\). Where \(m\) and \(n\) are the number of rows and columns of the matrix, respectively.

Python3JavaC++GoTypeScript

class Solution:
    def isPossibleToCutPath(self, grid: List[List[int]]) -> bool:
        def dfs(i, j):
            if i >= m or j >= n or grid[i][j] == 0:
                return False
            grid[i][j] = 0
            if i == m - 1 and j == n - 1:
                return True
            return dfs(i + 1, j) or dfs(i, j + 1)

        m, n = len(grid), len(grid[0])
        a = dfs(0, 0)
        grid[0][0] = grid[-1][-1] = 1
        b = dfs(0, 0)
        return not (a and b)

class Solution {
    private int[][] grid;
    private int m;
    private int n;

    public boolean isPossibleToCutPath(int[][] grid) {
        this.grid = grid;
        m = grid.length;
        n = grid[0].length;
        boolean a = dfs(0, 0);
        grid[0][0] = 1;
        grid[m - 1][n - 1] = 1;
        boolean b = dfs(0, 0);
        return !(a && b);
    }

    private boolean dfs(int i, int j) {
        if (i >= m || j >= n || grid[i][j] == 0) {
            return false;
        }
        if (i == m - 1 && j == n - 1) {
            return true;
        }
        grid[i][j] = 0;
        return dfs(i + 1, j) || dfs(i, j + 1);
    }
}

class Solution {
public:
    bool isPossibleToCutPath(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        function<bool(int, int)> dfs = [&](int i, int j) -> bool {
            if (i >= m || j >= n || grid[i][j] == 0) {
                return false;
            }
            if (i == m - 1 && j == n - 1) {
                return true;
            }
            grid[i][j] = 0;
            return dfs(i + 1, j) || dfs(i, j + 1);
        };
        bool a = dfs(0, 0);
        grid[0][0] = grid[m - 1][n - 1] = 1;
        bool b = dfs(0, 0);
        return !(a && b);
    }
};

func isPossibleToCutPath(grid [][]int) bool {
    m, n := len(grid), len(grid[0])
    var dfs func(i, j int) bool
    dfs = func(i, j int) bool {
        if i >= m || j >= n || grid[i][j] == 0 {
            return false
        }
        if i == m-1 && j == n-1 {
            return true
        }
        grid[i][j] = 0
        return dfs(i+1, j) || dfs(i, j+1)
    }
    a := dfs(0, 0)
    grid[0][0], grid[m-1][n-1] = 1, 1
    b := dfs(0, 0)
    return !(a && b)
}

function isPossibleToCutPath(grid: number[][]): boolean {
    const m = grid.length;
    const n = grid[0].length;

    const dfs = (i: number, j: number): boolean => {
        if (i >= m || j >= n || grid[i][j] !== 1) {
            return false;
        }
        grid[i][j] = 0;
        if (i === m - 1 && j === n - 1) {
            return true;
        }
        return dfs(i + 1, j) || dfs(i, j + 1);
    };
    const a = dfs(0, 0);
    grid[0][0] = 1;
    grid[m - 1][n - 1] = 1;
    const b = dfs(0, 0);
    return !(a && b);
}

2556. Disconnect Path in a Binary Matrix by at Most One Flip

Description

Solutions

Solution 1: Two DFS Traversals

Comments