2500. Delete Greatest Value in Each Row

Description

You are given an m x n matrix grid consisting of positive integers.

Perform the following operation until grid becomes empty:

Delete the element with the greatest value from each row. If multiple such elements exist, delete any of them.
Add the maximum of deleted elements to the answer.

Note that the number of columns decreases by one after each operation.

Return the answer after performing the operations described above.

Example 1:

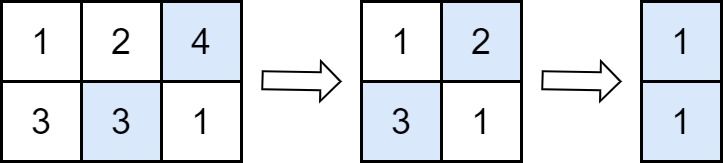
Input: grid = [[1,2,4],[3,3,1]]
Output: 8
Explanation: The diagram above shows the removed values in each step.
- In the first operation, we remove 4 from the first row and 3 from the second row (notice that, there are two cells with value 3 and we can remove any of them). We add 4 to the answer.
- In the second operation, we remove 2 from the first row and 3 from the second row. We add 3 to the answer.
- In the third operation, we remove 1 from the first row and 1 from the second row. We add 1 to the answer.
The final answer = 4 + 3 + 1 = 8.

Example 2:

Input: grid = [[10]]
Output: 10
Explanation: The diagram above shows the removed values in each step.
- In the first operation, we remove 10 from the first row. We add 10 to the answer.
The final answer = 10.

Constraints:

m == grid.length
n == grid[i].length
1 <= m, n <= 50
1 <= grid[i][j] <= 100

Solutions

Solution 1: Sorting

Since each operation involves removing the maximum value from each row and then adding the maximum value to the answer, we can first sort each row.

Next, we traverse each column, take the maximum value from each column, and add it to the answer.

The time complexity is $O(m \times n \times \log n)$, and the space complexity is $O(\log n)$. Here, $m$ and $n$ are the number of rows and columns of the matrix, respectively.

Python3JavaC++GoTypeScriptRust

class Solution:
    def deleteGreatestValue(self, grid: List[List[int]]) -> int:
        for row in grid:
            row.sort()
        return sum(max(col) for col in zip(*grid))

class Solution {
    public int deleteGreatestValue(int[][] grid) {
        for (var row : grid) {
            Arrays.sort(row);
        }
        int ans = 0;
        for (int j = 0; j < grid[0].length; ++j) {
            int t = 0;
            for (int i = 0; i < grid.length; ++i) {
                t = Math.max(t, grid[i][j]);
            }
            ans += t;
        }
        return ans;
    }
}

class Solution {
public:
    int deleteGreatestValue(vector<vector<int>>& grid) {
        for (auto& row : grid) {
            ranges::sort(row);
        }
        int ans = 0;
        for (int j = 0; j < grid[0].size(); ++j) {
            int t = 0;
            for (int i = 0; i < grid.size(); ++i) {
                t = max(t, grid[i][j]);
            }
            ans += t;
        }
        return ans;
    }
};

func deleteGreatestValue(grid [][]int) (ans int) {
    for _, row := range grid {
        sort.Ints(row)
    }
    for j := range grid[0] {
        t := 0
        for i := range grid {
            if t < grid[i][j] {
                t = grid[i][j]
            }
        }
        ans += t
    }
    return
}

function deleteGreatestValue(grid: number[][]): number {
    for (const row of grid) {
        row.sort((a, b) => a - b);
    }

    let ans = 0;
    for (let j = 0; j < grid[0].length; ++j) {
        let t = 0;
        for (let i = 0; i < grid.length; ++i) {
            t = Math.max(t, grid[i][j]);
        }
        ans += t;
    }

    return ans;
}

impl Solution {
    pub fn delete_greatest_value(grid: Vec<Vec<i32>>) -> i32 {
        let mut grid = grid;
        for i in 0..grid.len() {
            grid[i].sort();
        }

        let mut ans = 0;
        for j in 0..grid[0].len() {
            let mut mx = 0;

            for i in 0..grid.len() {
                if grid[i][j] > mx {
                    mx = grid[i][j];
                }
            }

            ans += mx;
        }

        ans
    }
}

2500. Delete Greatest Value in Each Row

Description

Solutions

Solution 1: Sorting

Comments