2493. Divide Nodes Into the Maximum Number of Groups

Description

You are given a positive integer n representing the number of nodes in an undirected graph. The nodes are labeled from 1 to n.

You are also given a 2D integer array edges, where edges[i] = [ai, bi] indicates that there is a bidirectional edge between nodes ai and bi. Notice that the given graph may be disconnected.

Divide the nodes of the graph into m groups (1-indexed) such that:

• Each node in the graph belongs to exactly one group.
• For every pair of nodes in the graph that are connected by an edge [ai, bi], if ai belongs to the group with index x, and bi belongs to the group with index y, then |y - x| = 1.

Return the maximum number of groups (i.e., maximum m) into which you can divide the nodes. Return -1 if it is impossible to group the nodes with the given conditions.

 

Example 1:

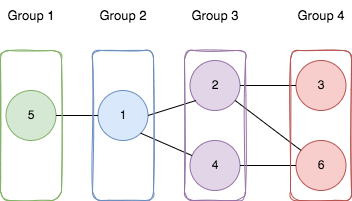
Input: n = 6, edges = [[1,2],[1,4],[1,5],[2,6],[2,3],[4,6]]
Output: 4
Explanation: As shown in the image we:
- Add node 5 to the first group.
- Add node 1 to the second group.
- Add nodes 2 and 4 to the third group.
- Add nodes 3 and 6 to the fourth group.
We can see that every edge is satisfied.
It can be shown that that if we create a fifth group and move any node from the third or fourth group to it, at least on of the edges will not be satisfied.

Example 2:

Input: n = 3, edges = [[1,2],[2,3],[3,1]]
Output: -1
Explanation: If we add node 1 to the first group, node 2 to the second group, and node 3 to the third group to satisfy the first two edges, we can see that the third edge will not be satisfied.
It can be shown that no grouping is possible.

 

Constraints:

• 1 <= n <= 500
• 1 <= edges.length <= 104
• edges[i].length == 2
• 1 <= ai, bi <= n
• ai != bi
• There is at most one edge between any pair of vertices.

Solutions

Solution 1: BFS + Enumeration

Given that the graph provided by the problem may be disconnected, we need to process each connected component, find the maximum number of groups in each connected component, and accumulate them to get the final result.

We can enumerate each node as the node of the first group, then use BFS to traverse the entire connected component, and use an array $d$ to record the maximum number of groups in each connected component. In the code implementation, we use the smallest node in the connected component as the root node of this connected component.

During the BFS process, we use a queue $q$ to store the nodes currently traversed, use an array $dist$ to record the distance from each node to the starting node, use a variable $mx$ to record the maximum depth of the current connected component, and use a variable $root$ to record the root node of the current connected component.

During the traversal, if we find that the $dist[b]$ of a certain node $b$ is $0$, it means that $b$ has not been traversed yet. We set the distance of $b$ to $dist[a] + 1$, update $mx$, and add $b$ to the queue $q$. If the distance of $b$ has been updated, we check whether the distance between $b$ and $a$ is $1$. If not, it means that the problem requirements cannot be met, so we directly return $-1$.

The time complexity is $O(n \times (n + m))$, and the space complexity is $O(n + m)$. Where $n$ and $m$ are the number of nodes and edges respectively.

Python3JavaC++GoJavaScript

class Solution:
    def magnificentSets(self, n: int, edges: List[List[int]]) -> int:
        g = [[] for _ in range(n)]
        for a, b in edges:
            g[a - 1].append(b - 1)
            g[b - 1].append(a - 1)
        d = defaultdict(int)
        for i in range(n):
            q = deque([i])
            dist = [0] * n
            dist[i] = mx = 1
            root = i
            while q:
                a = q.popleft()
                root = min(root, a)
                for b in g[a]:
                    if dist[b] == 0:
                        dist[b] = dist[a] + 1
                        mx = max(mx, dist[b])
                        q.append(b)
                    elif abs(dist[b] - dist[a]) != 1:
                        return -1
            d[root] = max(d[root], mx)
        return sum(d.values())

class Solution {
    public int magnificentSets(int n, int[][] edges) {
        List<Integer>[] g = new List[n];
        Arrays.setAll(g, k -> new ArrayList<>());
        for (var e : edges) {
            int a = e[0] - 1, b = e[1] - 1;
            g[a].add(b);
            g[b].add(a);
        }
        int[] d = new int[n];
        int[] dist = new int[n];
        for (int i = 0; i < n; ++i) {
            Deque<Integer> q = new ArrayDeque<>();
            q.offer(i);
            Arrays.fill(dist, 0);
            dist[i] = 1;
            int mx = 1;
            int root = i;
            while (!q.isEmpty()) {
                int a = q.poll();
                root = Math.min(root, a);
                for (int b : g[a]) {
                    if (dist[b] == 0) {
                        dist[b] = dist[a] + 1;
                        mx = Math.max(mx, dist[b]);
                        q.offer(b);
                    } else if (Math.abs(dist[b] - dist[a]) != 1) {
                        return -1;
                    }
                }
            }
            d[root] = Math.max(d[root], mx);
        }
        return Arrays.stream(d).sum();
    }
}

class Solution {
public:
    int magnificentSets(int n, vector<vector<int>>& edges) {
        vector<int> g[n];
        for (auto& e : edges) {
            int a = e[0] - 1, b = e[1] - 1;
            g[a].push_back(b);
            g[b].push_back(a);
        }
        vector<int> d(n);
        for (int i = 0; i < n; ++i) {
            queue<int> q{{i}};
            vector<int> dist(n);
            dist[i] = 1;
            int mx = 1;
            int root = i;
            while (q.size()) {
                int a = q.front();
                q.pop();
                root = min(root, a);
                for (int b : g[a]) {
                    if (dist[b] == 0) {
                        dist[b] = dist[a] + 1;
                        mx = max(mx, dist[b]);
                        q.push(b);
                    } else if (abs(dist[b] - dist[a]) != 1) {
                        return -1;
                    }
                }
            }
            d[root] = max(d[root], mx);
        }
        return accumulate(d.begin(), d.end(), 0);
    }
};

func magnificentSets(n int, edges [][]int) (ans int) {
    g := make([][]int, n)
    for _, e := range edges {
        a, b := e[0]-1, e[1]-1
        g[a] = append(g[a], b)
        g[b] = append(g[b], a)
    }
    d := make([]int, n)
    for i := range d {
        q := []int{i}
        dist := make([]int, n)
        dist[i] = 1
        mx := 1
        root := i
        for len(q) > 0 {
            a := q[0]
            q = q[1:]
            root = min(root, a)
            for _, b := range g[a] {
                if dist[b] == 0 {
                    dist[b] = dist[a] + 1
                    mx = max(mx, dist[b])
                    q = append(q, b)
                } else if abs(dist[b]-dist[a]) != 1 {
                    return -1
                }
            }
        }
        d[root] = max(d[root], mx)
    }
    for _, x := range d {
        ans += x
    }
    return
}

func abs(x int) int {
    if x < 0 {
        return -x
    }
    return x
}

/**
 * @param {number} n
 * @param {number[][]} edges
 * @return {number}
 */
var magnificentSets = function (n, edges) {
    const g = Array.from({ length: n }, () => []);
    for (const [a, b] of edges) {
        g[a - 1].push(b - 1);
        g[b - 1].push(a - 1);
    }
    const d = Array(n).fill(0);
    for (let i = 0; i < n; ++i) {
        const q = [i];
        const dist = Array(n).fill(0);
        dist[i] = 1;
        let mx = 1;
        let root = i;
        while (q.length) {
            const a = q.shift();
            root = Math.min(root, a);
            for (const b of g[a]) {
                if (dist[b] === 0) {
                    dist[b] = dist[a] + 1;
                    mx = Math.max(mx, dist[b]);
                    q.push(b);
                } else if (Math.abs(dist[b] - dist[a]) !== 1) {
                    return -1;
                }
            }
        }
        d[root] = Math.max(d[root], mx);
    }
    return d.reduce((a, b) => a + b);
};

Comments