Depth-First Search
Graph
Tree
Trie
Description
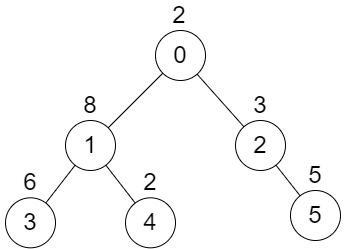
There is an undirected tree with n nodes labeled from 0 to n - 1. You are given the integer n and a 2D integer array edges of length n - 1, where edges[i] = [ai , bi ] indicates that there is an edge between nodes ai and bi in the tree. The root of the tree is the node labeled 0.
Each node has an associated value . You are given an array values of length n, where values[i] is the value of the ith node.
Select any two non-overlapping subtrees. Your score is the bitwise XOR of the sum of the values within those subtrees.
Return the maximum possible score you can achieve . If it is impossible to find two nonoverlapping subtrees , return 0.
Note that:
The subtree of a node is the tree consisting of that node and all of its descendants.
Two subtrees are non-overlapping if they do not share any common node.
Example 1:
Input: n = 6, edges = [[0,1],[0,2],[1,3],[1,4],[2,5]], values = [2,8,3,6,2,5]
Output: 24
Explanation: Node 1's subtree has sum of values 16, while node 2's subtree has sum of values 8, so choosing these nodes will yield a score of 16 XOR 8 = 24. It can be proved that is the maximum possible score we can obtain.
Example 2:
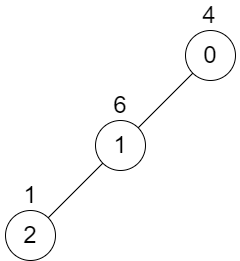
Input: n = 3, edges = [[0,1],[1,2]], values = [4,6,1]
Output: 0
Explanation: There is no possible way to select two non-overlapping subtrees, so we just return 0.
Constraints:
2 <= n <= 5 * 104 edges.length == n - 10 <= ai , bi < nvalues.length == n1 <= values[i] <= 109 It is guaranteed that edges represents a valid tree.
Solutions
Solution 1
Python3 Java C++ Go
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56 class Trie :
def __init__ ( self ):
self . children = [ None ] * 2
def insert ( self , x ):
node = self
for i in range ( 47 , - 1 , - 1 ):
v = ( x >> i ) & 1
if node . children [ v ] is None :
node . children [ v ] = Trie ()
node = node . children [ v ]
def search ( self , x ):
node = self
res = 0
for i in range ( 47 , - 1 , - 1 ):
v = ( x >> i ) & 1
if node is None :
return res
if node . children [ v ^ 1 ]:
res = res << 1 | 1
node = node . children [ v ^ 1 ]
else :
res <<= 1
node = node . children [ v ]
return res
class Solution :
def maxXor ( self , n : int , edges : List [ List [ int ]], values : List [ int ]) -> int :
def dfs1 ( i , fa ):
t = values [ i ]
for j in g [ i ]:
if j != fa :
t += dfs1 ( j , i )
s [ i ] = t
return t
def dfs2 ( i , fa ):
nonlocal ans
ans = max ( ans , tree . search ( s [ i ]))
for j in g [ i ]:
if j != fa :
dfs2 ( j , i )
tree . insert ( s [ i ])
g = defaultdict ( list )
for a , b in edges :
g [ a ] . append ( b )
g [ b ] . append ( a )
s = [ 0 ] * n
dfs1 ( 0 , - 1 )
ans = 0
tree = Trie ()
dfs2 ( 0 , - 1 )
return ans
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78 class Trie {
Trie [] children = new Trie [ 2 ] ;
void insert ( long x ) {
Trie node = this ;
for ( int i = 47 ; i >= 0 ; -- i ) {
int v = ( int ) ( x >> i ) & 1 ;
if ( node . children [ v ] == null ) {
node . children [ v ] = new Trie ();
}
node = node . children [ v ] ;
}
}
long search ( long x ) {
Trie node = this ;
long res = 0 ;
for ( int i = 47 ; i >= 0 ; -- i ) {
int v = ( int ) ( x >> i ) & 1 ;
if ( node == null ) {
return res ;
}
if ( node . children [ v ^ 1 ] != null ) {
res = res << 1 | 1 ;
node = node . children [ v ^ 1 ] ;
} else {
res <<= 1 ;
node = node . children [ v ] ;
}
}
return res ;
}
}
class Solution {
private List < Integer >[] g ;
private int [] vals ;
private long [] s ;
private Trie tree ;
private long ans ;
public long maxXor ( int n , int [][] edges , int [] values ) {
g = new List [ n ] ;
s = new long [ n ] ;
vals = values ;
Arrays . setAll ( g , k -> new ArrayList <> ());
for ( var e : edges ) {
int a = e [ 0 ] , b = e [ 1 ] ;
g [ a ] . add ( b );
g [ b ] . add ( a );
}
dfs1 ( 0 , - 1 );
tree = new Trie ();
dfs2 ( 0 , - 1 );
return ans ;
}
private void dfs2 ( int i , int fa ) {
ans = Math . max ( ans , tree . search ( s [ i ] ));
for ( int j : g [ i ] ) {
if ( j != fa ) {
dfs2 ( j , i );
}
}
tree . insert ( s [ i ] );
}
private long dfs1 ( int i , int fa ) {
long t = vals [ i ] ;
for ( int j : g [ i ] ) {
if ( j != fa ) {
t += dfs1 ( j , i );
}
}
s [ i ] = t ;
return t ;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70 using ll = long long ;
class Trie {
public :
vector < Trie *> children ;
string v ;
Trie ()
: children ( 2 ) {}
void insert ( ll x ) {
Trie * node = this ;
for ( int i = 47 ; ~ i ; -- i ) {
int v = ( x >> i ) & 1 ;
if ( ! node -> children [ v ]) node -> children [ v ] = new Trie ();
node = node -> children [ v ];
}
}
ll search ( ll x ) {
Trie * node = this ;
ll res = 0 ;
for ( int i = 47 ; ~ i ; -- i ) {
if ( ! node ) return res ;
int v = ( x >> i ) & 1 ;
if ( node -> children [ v ^ 1 ]) {
res = res << 1 | 1 ;
node = node -> children [ v ^ 1 ];
} else {
res <<= 1 ;
node = node -> children [ v ];
}
}
return res ;
}
};
class Solution {
public :
long long maxXor ( int n , vector < vector < int >>& edges , vector < int >& values ) {
vector < vector < int >> g ( n );
for ( auto & e : edges ) {
int a = e [ 0 ], b = e [ 1 ];
g [ a ]. emplace_back ( b );
g [ b ]. emplace_back ( a );
}
vector < ll > s ( n );
function < ll ( int , int ) > dfs1 = [ & ]( int i , int fa ) -> ll {
ll t = values [ i ];
for ( int j : g [ i ]) {
if ( j != fa ) t += dfs1 ( j , i );
}
s [ i ] = t ;
return t ;
};
dfs1 ( 0 , -1 );
Trie tree ;
ll ans = 0 ;
function < void ( int , int ) > dfs2 = [ & ]( int i , int fa ) {
ans = max ( ans , tree . search ( s [ i ]));
for ( int j : g [ i ]) {
if ( j != fa ) {
dfs2 ( j , i );
}
}
tree . insert ( s [ i ]);
};
dfs2 ( 0 , -1 );
return ans ;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73 type Trie struct {
children [ 2 ] * Trie
}
func newTrie () * Trie {
return & Trie {}
}
func ( this * Trie ) insert ( x int ) {
node := this
for i := 47 ; i >= 0 ; i -- {
v := ( x >> i ) & 1
if node . children [ v ] == nil {
node . children [ v ] = newTrie ()
}
node = node . children [ v ]
}
}
func ( this * Trie ) search ( x int ) int {
node := this
res := 0
for i := 47 ; i >= 0 ; i -- {
v := ( x >> i ) & 1
if node == nil {
return res
}
if node . children [ v ^ 1 ] != nil {
res = res << 1 | 1
node = node . children [ v ^ 1 ]
} else {
res <<= 1
node = node . children [ v ]
}
}
return res
}
func maxXor ( n int , edges [][] int , values [] int ) int64 {
g := make ([][] int , n )
for _ , e := range edges {
a , b := e [ 0 ], e [ 1 ]
g [ a ] = append ( g [ a ], b )
g [ b ] = append ( g [ b ], a )
}
s := make ([] int , n )
var dfs1 func ( i , fa int ) int
dfs1 = func ( i , fa int ) int {
t := values [ i ]
for _ , j := range g [ i ] {
if j != fa {
t += dfs1 ( j , i )
}
}
s [ i ] = t
return t
}
dfs1 ( 0 , - 1 )
ans := 0
tree := newTrie ()
var dfs2 func ( i , fa int )
dfs2 = func ( i , fa int ) {
ans = max ( ans , tree . search ( s [ i ]))
for _ , j := range g [ i ] {
if j != fa {
dfs2 ( j , i )
}
}
tree . insert ( s [ i ])
}
dfs2 ( 0 , - 1 )
return int64 ( ans )
}
GitHub