Skip to content

2361. Minimum Costs Using the Train Line πŸ”’

Description

A train line going through a city has two routes, the regular route and the express route. Both routes go through the same n + 1 stops labeled from 0 to n. Initially, you start on the regular route at stop 0.

You are given two 1-indexed integer arrays regular and express, both of length n. regular[i] describes the cost it takes to go from stop i - 1 to stop i using the regular route, and express[i] describes the cost it takes to go from stop i - 1 to stop i using the express route.

You are also given an integer expressCost which represents the cost to transfer from the regular route to the express route.

Note that:

  • There is no cost to transfer from the express route back to the regular route.
  • You pay expressCost every time you transfer from the regular route to the express route.
  • There is no extra cost to stay on the express route.

Return a 1-indexed array costs of length n, where costs[i] is the minimum cost to reach stop i from stop 0.

Note that a stop can be counted as reached from either route.

 

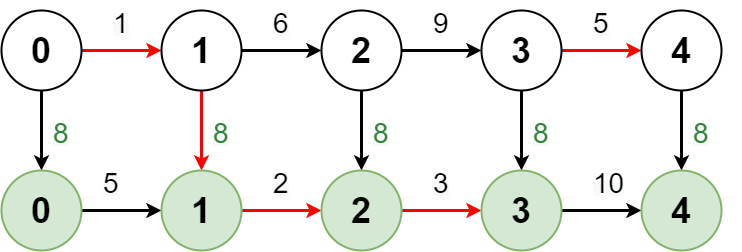
Example 1:

Input: regular = [1,6,9,5], express = [5,2,3,10], expressCost = 8
Output: [1,7,14,19]
Explanation: The diagram above shows how to reach stop 4 from stop 0 with minimum cost.
- Take the regular route from stop 0 to stop 1, costing 1.
- Take the express route from stop 1 to stop 2, costing 8 + 2 = 10.
- Take the express route from stop 2 to stop 3, costing 3.
- Take the regular route from stop 3 to stop 4, costing 5.
The total cost is 1 + 10 + 3 + 5 = 19.
Note that a different route could be taken to reach the other stops with minimum cost.

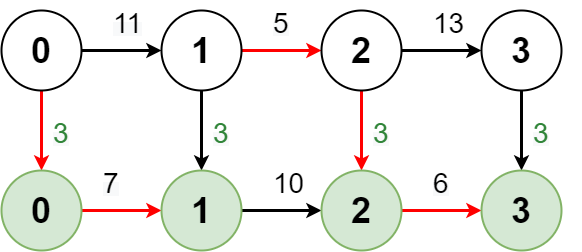
Example 2:

Input: regular = [11,5,13], express = [7,10,6], expressCost = 3
Output: [10,15,24]
Explanation: The diagram above shows how to reach stop 3 from stop 0 with minimum cost.
- Take the express route from stop 0 to stop 1, costing 3 + 7 = 10.
- Take the regular route from stop 1 to stop 2, costing 5.
- Take the express route from stop 2 to stop 3, costing 3 + 6 = 9.
The total cost is 10 + 5 + 9 = 24.
Note that the expressCost is paid again to transfer back to the express route.

 

Constraints:

  • n == regular.length == express.length
  • 1 <= n <= 105
  • 1 <= regular[i], express[i], expressCost <= 105

Solutions

Solution 1: Dynamic Programming

We define $f[i]$ as the minimum cost from station $0$ to station $i$ when arriving at station $i$ by the regular route, and $g[i]$ as the minimum cost from station $0$ to station $i$ when arriving at station $i$ by the express route. Initially, $f[0]=0, g[0]=\infty$.

Next, we consider how to transition the states of $f[i]$ and $g[i]$.

If we arrive at station $i$ by the regular route, we can either come from station $i-1$ by the regular route or switch from the express route at station $i-1$ to the regular route. Therefore, we can get the state transition equation:

$$ f[i]=\min{f[i-1]+a_i, g[i-1]+a_i} $$

where $a_i$ represents the cost of taking the regular route from station $i-1$ to station $i$.

If we arrive at station $i$ by the express route, we can either switch from the regular route at station $i-1$ to the express route or continue on the express route from station $i-1$. Therefore, we can get the state transition equation:

$$ g[i]=\min{f[i-1]+expressCost+b_i, g[i-1]+b_i} $$

where $b_i$ represents the cost of taking the express route from station $i-1$ to station $i$.

We denote the answer array as $cost$, where $cost[i]$ represents the minimum cost from station $0$ to station $i$. Since we can reach station $i$ from any route, we have $cost[i]=\min{f[i], g[i]}$.

Finally, we return $cost$.

The time complexity is $O(n)$ and the space complexity is $O(n)$, where $n$ is the number of stations.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
class Solution:
    def minimumCosts(
        self, regular: List[int], express: List[int], expressCost: int
    ) -> List[int]:
        n = len(regular)
        f = [0] * (n + 1)
        g = [inf] * (n + 1)
        cost = [0] * n
        for i, (a, b) in enumerate(zip(regular, express), 1):
            f[i] = min(f[i - 1] + a, g[i - 1] + a)
            g[i] = min(f[i - 1] + expressCost + b, g[i - 1] + b)
            cost[i - 1] = min(f[i], g[i])
        return cost

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
class Solution {
    public long[] minimumCosts(int[] regular, int[] express, int expressCost) {
        int n = regular.length;
        long[] f = new long[n + 1];
        long[] g = new long[n + 1];
        g[0] = 1 << 30;
        long[] cost = new long[n];
        for (int i = 1; i <= n; ++i) {
            int a = regular[i - 1];
            int b = express[i - 1];
            f[i] = Math.min(f[i - 1] + a, g[i - 1] + a);
            g[i] = Math.min(f[i - 1] + expressCost + b, g[i - 1] + b);
            cost[i - 1] = Math.min(f[i], g[i]);
        }
        return cost;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    vector<long long> minimumCosts(vector<int>& regular, vector<int>& express, int expressCost) {
        int n = regular.size();
        long long f[n + 1];
        long long g[n + 1];
        f[0] = 0;
        g[0] = 1 << 30;
        vector<long long> cost(n);
        for (int i = 1; i <= n; ++i) {
            int a = regular[i - 1];
            int b = express[i - 1];
            f[i] = min(f[i - 1] + a, g[i - 1] + a);
            g[i] = min(f[i - 1] + expressCost + b, g[i - 1] + b);
            cost[i - 1] = min(f[i], g[i]);
        }
        return cost;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
func minimumCosts(regular []int, express []int, expressCost int) []int64 {
    n := len(regular)
    f := make([]int, n+1)
    g := make([]int, n+1)
    g[0] = 1 << 30
    cost := make([]int64, n)
    for i := 1; i <= n; i++ {
        a, b := regular[i-1], express[i-1]
        f[i] = min(f[i-1]+a, g[i-1]+a)
        g[i] = min(f[i-1]+expressCost+b, g[i-1]+b)
        cost[i-1] = int64(min(f[i], g[i]))
    }
    return cost
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
function minimumCosts(regular: number[], express: number[], expressCost: number): number[] {
    const n = regular.length;
    const f: number[] = new Array(n + 1).fill(0);
    const g: number[] = new Array(n + 1).fill(0);
    g[0] = 1 << 30;
    const cost: number[] = new Array(n).fill(0);
    for (let i = 1; i <= n; ++i) {
        const [a, b] = [regular[i - 1], express[i - 1]];
        f[i] = Math.min(f[i - 1] + a, g[i - 1] + a);
        g[i] = Math.min(f[i - 1] + expressCost + b, g[i - 1] + b);
        cost[i - 1] = Math.min(f[i], g[i]);
    }
    return cost;
}

We notice that in the state transition equations of $f[i]$ and $g[i]$, we only need to use $f[i-1]$ and $g[i-1]$. Therefore, we can use two variables $f$ and $g$ to record the values of $f[i-1]$ and $g[i-1]$ respectively. This allows us to optimize the space complexity to $O(1)$.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
class Solution:
    def minimumCosts(
        self, regular: List[int], express: List[int], expressCost: int
    ) -> List[int]:
        n = len(regular)
        f, g = 0, inf
        cost = [0] * n
        for i, (a, b) in enumerate(zip(regular, express), 1):
            ff = min(f + a, g + a)
            gg = min(f + expressCost + b, g + b)
            f, g = ff, gg
            cost[i - 1] = min(f, g)
        return cost

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
class Solution {
    public long[] minimumCosts(int[] regular, int[] express, int expressCost) {
        int n = regular.length;
        long f = 0;
        long g = 1 << 30;
        long[] cost = new long[n];
        for (int i = 0; i < n; ++i) {
            int a = regular[i];
            int b = express[i];
            long ff = Math.min(f + a, g + a);
            long gg = Math.min(f + expressCost + b, g + b);
            f = ff;
            g = gg;
            cost[i] = Math.min(f, g);
        }
        return cost;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    vector<long long> minimumCosts(vector<int>& regular, vector<int>& express, int expressCost) {
        int n = regular.size();
        long long f = 0;
        long long g = 1 << 30;
        vector<long long> cost(n);
        for (int i = 0; i < n; ++i) {
            int a = regular[i];
            int b = express[i];
            long long ff = min(f + a, g + a);
            long long gg = min(f + expressCost + b, g + b);
            f = ff;
            g = gg;
            cost[i] = min(f, g);
        }
        return cost;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
func minimumCosts(regular []int, express []int, expressCost int) []int64 {
    f, g := 0, 1<<30
    cost := make([]int64, len(regular))
    for i, a := range regular {
        b := express[i]
        ff := min(f+a, g+a)
        gg := min(f+expressCost+b, g+b)
        f, g = ff, gg
        cost[i] = int64(min(f, g))
    }
    return cost
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
function minimumCosts(regular: number[], express: number[], expressCost: number): number[] {
    const n = regular.length;
    let f = 0;
    let g = 1 << 30;
    const cost: number[] = new Array(n).fill(0);
    for (let i = 0; i < n; ++i) {
        const [a, b] = [regular[i], express[i]];
        const ff = Math.min(f + a, g + a);
        const gg = Math.min(f + expressCost + b, g + b);
        [f, g] = [ff, gg];
        cost[i] = Math.min(f, g);
    }
    return cost;
}

Comments