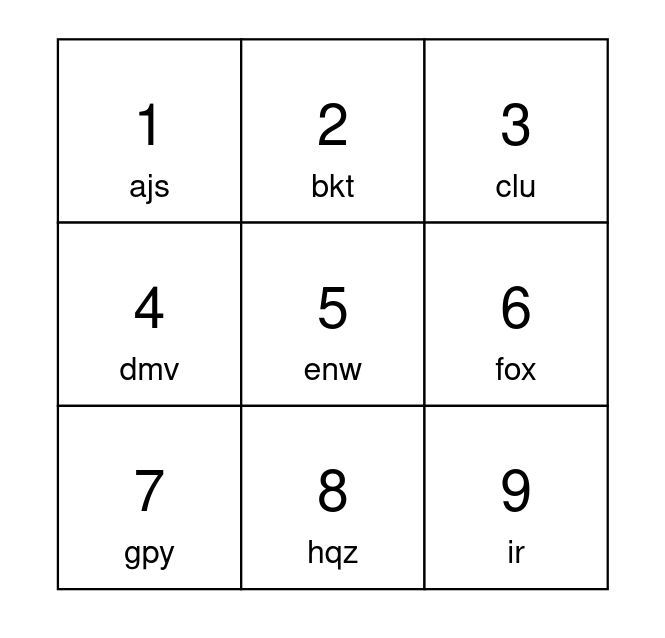
2268. Minimum Number of Keypresses 🔒

Description

You have a keypad with 9 buttons, numbered from 1 to 9, each mapped to lowercase English letters. You can choose which characters each button is matched to as long as:

All 26 lowercase English letters are mapped to.
Each character is mapped to by exactly 1 button.
Each button maps to at most 3 characters.

To type the first character matched to a button, you press the button once. To type the second character, you press the button twice, and so on.

Given a string s, return the minimum number of keypresses needed to type s using your keypad.

Note that the characters mapped to by each button, and the order they are mapped in cannot be changed.

Example 1:

Input: s = "apple"
Output: 5
Explanation: One optimal way to setup your keypad is shown above.
Type 'a' by pressing button 1 once.
Type 'p' by pressing button 6 once.
Type 'p' by pressing button 6 once.
Type 'l' by pressing button 5 once.
Type 'e' by pressing button 3 once.
A total of 5 button presses are needed, so return 5.

Example 2:

Input: s = "abcdefghijkl"
Output: 15
Explanation: One optimal way to setup your keypad is shown above.
The letters 'a' to 'i' can each be typed by pressing a button once.
Type 'j' by pressing button 1 twice.
Type 'k' by pressing button 2 twice.
Type 'l' by pressing button 3 twice.
A total of 15 button presses are needed, so return 15.

Constraints:

1 <= s.length <= 10⁵
s consists of lowercase English letters.

Solutions

Solution 1: Counting + Greedy

First, we count the occurrence of each character in the string \(s\), and record it in an array or hash table \(\textit{cnt}\).

The problem requires minimizing the number of key presses, so the \(9\) most frequent characters should correspond to keys \(1\) to \(9\), the \(10\)th to \(18\)th most frequent characters should correspond to keys \(1\) to \(9\) again, and so on.

Therefore, we can sort the values in \(\textit{cnt}\) in descending order, and then allocate them to the keys in the order from \(1\) to \(9\), adding \(1\) to the number of key presses after allocating every \(9\) characters.

Python3JavaC++GoTypeScript

class Solution:
    def minimumKeypresses(self, s: str) -> int:
        cnt = Counter(s)
        ans, k = 0, 1
        for i, x in enumerate(sorted(cnt.values(), reverse=True), 1):
            ans += k * x
            if i % 9 == 0:
                k += 1
        return ans

class Solution {
    public int minimumKeypresses(String s) {
        int[] cnt = new int[26];
        for (int i = 0; i < s.length(); ++i) {
            ++cnt[s.charAt(i) - 'a'];
        }
        Arrays.sort(cnt);
        int ans = 0, k = 1;
        for (int i = 1; i <= 26; ++i) {
            ans += k * cnt[26 - i];
            if (i % 9 == 0) {
                ++k;
            }
        }
        return ans;
    }
}

class Solution {
public:
    int minimumKeypresses(string s) {
        int cnt[26]{};
        for (char& c : s) {
            ++cnt[c - 'a'];
        }
        sort(begin(cnt), end(cnt), greater<int>());
        int ans = 0, k = 1;
        for (int i = 1; i <= 26; ++i) {
            ans += k * cnt[i - 1];
            if (i % 9 == 0) {
                ++k;
            }
        }
        return ans;
    }
};

func minimumKeypresses(s string) (ans int) {
    cnt := make([]int, 26)
    for _, c := range s {
        cnt[c-'a']++
    }
    sort.Ints(cnt)
    k := 1
    for i := 1; i <= 26; i++ {
        ans += k * cnt[26-i]
        if i%9 == 0 {
            k++
        }
    }
    return
}

function minimumKeypresses(s: string): number {
    const cnt: number[] = Array(26).fill(0);
    const a = 'a'.charCodeAt(0);
    for (const c of s) {
        ++cnt[c.charCodeAt(0) - a];
    }
    cnt.sort((a, b) => b - a);
    let [ans, k] = [0, 1];
    for (let i = 1; i <= 26; ++i) {
        ans += k * cnt[i - 1];
        if (i % 9 === 0) {
            ++k;
        }
    }
    return ans;
}

2268. Minimum Number of Keypresses 🔒

Description

Solutions

Solution 1: Counting + Greedy

Comments