Skip to content

223. Rectangle Area

Description

Given the coordinates of two rectilinear rectangles in a 2D plane, return the total area covered by the two rectangles.

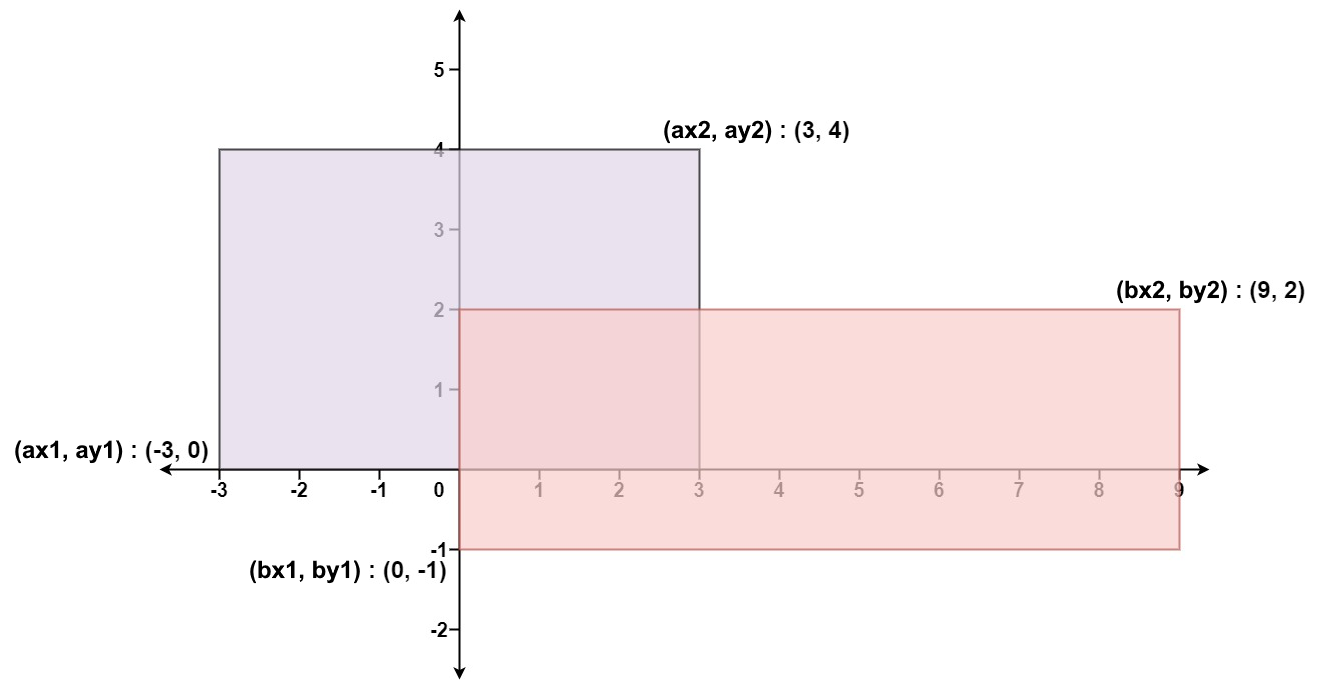
The first rectangle is defined by its bottom-left corner (ax1, ay1) and its top-right corner (ax2, ay2).

The second rectangle is defined by its bottom-left corner (bx1, by1) and its top-right corner (bx2, by2).

 

Example 1:

Rectangle Area

Input: ax1 = -3, ay1 = 0, ax2 = 3, ay2 = 4, bx1 = 0, by1 = -1, bx2 = 9, by2 = 2
Output: 45

Example 2:

Input: ax1 = -2, ay1 = -2, ax2 = 2, ay2 = 2, bx1 = -2, by1 = -2, bx2 = 2, by2 = 2
Output: 16

 

Constraints:

  • -104 <= ax1 <= ax2 <= 104
  • -104 <= ay1 <= ay2 <= 104
  • -104 <= bx1 <= bx2 <= 104
  • -104 <= by1 <= by2 <= 104

Solutions

Solution 1: Calculate Overlapping Area

First, we calculate the area of the two rectangles separately, denoted as $a$ and $b$. Then we calculate the overlapping width $width$ and height $height$. The overlapping area is $max(width, 0) \times max(height, 0)$. Finally, we subtract the overlapping area from $a$ and $b$.

The time complexity is $O(1)$, and the space complexity is $O(1)$.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
class Solution:
    def computeArea(
        self,
        ax1: int,
        ay1: int,
        ax2: int,
        ay2: int,
        bx1: int,
        by1: int,
        bx2: int,
        by2: int,
    ) -> int:
        a = (ax2 - ax1) * (ay2 - ay1)
        b = (bx2 - bx1) * (by2 - by1)
        width = min(ax2, bx2) - max(ax1, bx1)
        height = min(ay2, by2) - max(ay1, by1)
        return a + b - max(height, 0) * max(width, 0)

1
2
3
4
5
6
7
8
9
class Solution {
    public int computeArea(int ax1, int ay1, int ax2, int ay2, int bx1, int by1, int bx2, int by2) {
        int a = (ax2 - ax1) * (ay2 - ay1);
        int b = (bx2 - bx1) * (by2 - by1);
        int width = Math.min(ax2, bx2) - Math.max(ax1, bx1);
        int height = Math.min(ay2, by2) - Math.max(ay1, by1);
        return a + b - Math.max(height, 0) * Math.max(width, 0);
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
class Solution {
public:
    int computeArea(int ax1, int ay1, int ax2, int ay2, int bx1, int by1, int bx2, int by2) {
        int a = (ax2 - ax1) * (ay2 - ay1);
        int b = (bx2 - bx1) * (by2 - by1);
        int width = min(ax2, bx2) - max(ax1, bx1);
        int height = min(ay2, by2) - max(ay1, by1);
        return a + b - max(height, 0) * max(width, 0);
    }
};

1
2
3
4
5
6
7
func computeArea(ax1 int, ay1 int, ax2 int, ay2 int, bx1 int, by1 int, bx2 int, by2 int) int {
    a := (ax2 - ax1) * (ay2 - ay1)
    b := (bx2 - bx1) * (by2 - by1)
    width := min(ax2, bx2) - max(ax1, bx1)
    height := min(ay2, by2) - max(ay1, by1)
    return a + b - max(height, 0)*max(width, 0)
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
function computeArea(
    ax1: number,
    ay1: number,
    ax2: number,
    ay2: number,
    bx1: number,
    by1: number,
    bx2: number,
    by2: number,
): number {
    const a = (ax2 - ax1) * (ay2 - ay1);
    const b = (bx2 - bx1) * (by2 - by1);
    const width = Math.min(ax2, bx2) - Math.max(ax1, bx1);
    const height = Math.min(ay2, by2) - Math.max(ay1, by1);
    return a + b - Math.max(width, 0) * Math.max(height, 0);
}

1
2
3
4
5
6
7
8
9
public class Solution {
    public int ComputeArea(int ax1, int ay1, int ax2, int ay2, int bx1, int by1, int bx2, int by2) {
        int a = (ax2 - ax1) * (ay2 - ay1);
        int b = (bx2 - bx1) * (by2 - by1);
        int width = Math.Min(ax2, bx2) - Math.Max(ax1, bx1);
        int height = Math.Min(ay2, by2) - Math.Max(ay1, by1);
        return a + b - Math.Max(height, 0) * Math.Max(width, 0);
    }
}

Comments