Skip to content

221. Maximal Square

Description

Given an m x n binary matrix filled with 0's and 1's, find the largest square containing only 1's and return its area.

 

Example 1:

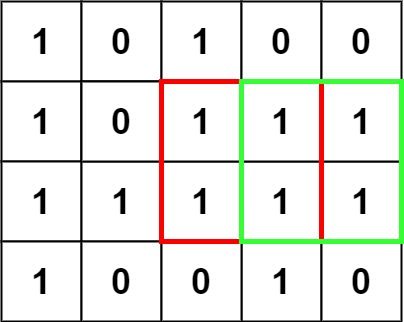
Input: matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
Output: 4

Example 2:

Input: matrix = [["0","1"],["1","0"]]
Output: 1

Example 3:

Input: matrix = [["0"]]
Output: 0

 

Constraints:

  • m == matrix.length
  • n == matrix[i].length
  • 1 <= m, n <= 300
  • matrix[i][j] is '0' or '1'.

Solutions

Solution 1: Dynamic Programming

We define $dp[i + 1][j + 1]$ as the maximum square side length with the lower right corner at index $(i, j)$. The answer is the maximum value among all $dp[i + 1][j + 1]$.

The state transition equation is:

$$ dp[i + 1][j + 1] = \begin{cases} 0 & \textit{if } matrix[i][j] = '0' \ \min(dp[i][j], dp[i][j + 1], dp[i + 1][j]) + 1 & \textit{if } matrix[i][j] = '1' \end{cases} $$

The time complexity is $O(m\times n)$, and the space complexity is $O(m\times n)$. Where $m$ and $n$ are the number of rows and columns of the matrix, respectively.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
class Solution:
    def maximalSquare(self, matrix: List[List[str]]) -> int:
        m, n = len(matrix), len(matrix[0])
        dp = [[0] * (n + 1) for _ in range(m + 1)]
        mx = 0
        for i in range(m):
            for j in range(n):
                if matrix[i][j] == '1':
                    dp[i + 1][j + 1] = min(dp[i][j + 1], dp[i + 1][j], dp[i][j]) + 1
                    mx = max(mx, dp[i + 1][j + 1])
        return mx * mx

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
class Solution {
    public int maximalSquare(char[][] matrix) {
        int m = matrix.length, n = matrix[0].length;
        int[][] dp = new int[m + 1][n + 1];
        int mx = 0;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (matrix[i][j] == '1') {
                    dp[i + 1][j + 1] = Math.min(Math.min(dp[i][j + 1], dp[i + 1][j]), dp[i][j]) + 1;
                    mx = Math.max(mx, dp[i + 1][j + 1]);
                }
            }
        }
        return mx * mx;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
class Solution {
public:
    int maximalSquare(vector<vector<char>>& matrix) {
        int m = matrix.size(), n = matrix[0].size();
        vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
        int mx = 0;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (matrix[i][j] == '1') {
                    dp[i + 1][j + 1] = min(min(dp[i][j + 1], dp[i + 1][j]), dp[i][j]) + 1;
                    mx = max(mx, dp[i + 1][j + 1]);
                }
            }
        }
        return mx * mx;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
func maximalSquare(matrix [][]byte) int {
    m, n := len(matrix), len(matrix[0])
    dp := make([][]int, m+1)
    for i := 0; i <= m; i++ {
        dp[i] = make([]int, n+1)
    }
    mx := 0
    for i := 0; i < m; i++ {
        for j := 0; j < n; j++ {
            if matrix[i][j] == '1' {
                dp[i+1][j+1] = min(min(dp[i][j+1], dp[i+1][j]), dp[i][j]) + 1
                mx = max(mx, dp[i+1][j+1])
            }
        }
    }
    return mx * mx
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
public class Solution {
    public int MaximalSquare(char[][] matrix) {
        int m = matrix.Length, n = matrix[0].Length;
        var dp = new int[m + 1, n + 1];
        int mx = 0;
        for (int i = 0; i < m; ++i)
        {
            for (int j = 0; j < n; ++j)
            {
                if (matrix[i][j] == '1')
                {
                    dp[i + 1, j + 1] = Math.Min(Math.Min(dp[i, j + 1], dp[i + 1, j]), dp[i, j]) + 1;
                    mx = Math.Max(mx, dp[i + 1, j + 1]);
                }
            }
        }
        return mx * mx;
    }
}

Comments