2204. Distance to a Cycle in Undirected Graph 🔒

Description

You are given a positive integer n representing the number of nodes in a connected undirected graph containing exactly one cycle. The nodes are numbered from 0 to n - 1 (inclusive).

You are also given a 2D integer array edges, where edges[i] = [node1_i, node2_i] denotes that there is a bidirectional edge connecting node1_i and node2_i in the graph.

The distance between two nodes a and b is defined to be the minimum number of edges that are needed to go from a to b.

Return an integer array answer of size n, where answer[i] is the minimum distance between the i^th node and any node in the cycle.

Example 1:

Input: n = 7, edges = [[1,2],[2,4],[4,3],[3,1],[0,1],[5,2],[6,5]]
Output: [1,0,0,0,0,1,2]
Explanation:
The nodes 1, 2, 3, and 4 form the cycle.
The distance from 0 to 1 is 1.
The distance from 1 to 1 is 0.
The distance from 2 to 2 is 0.
The distance from 3 to 3 is 0.
The distance from 4 to 4 is 0.
The distance from 5 to 2 is 1.
The distance from 6 to 2 is 2.

Example 2:

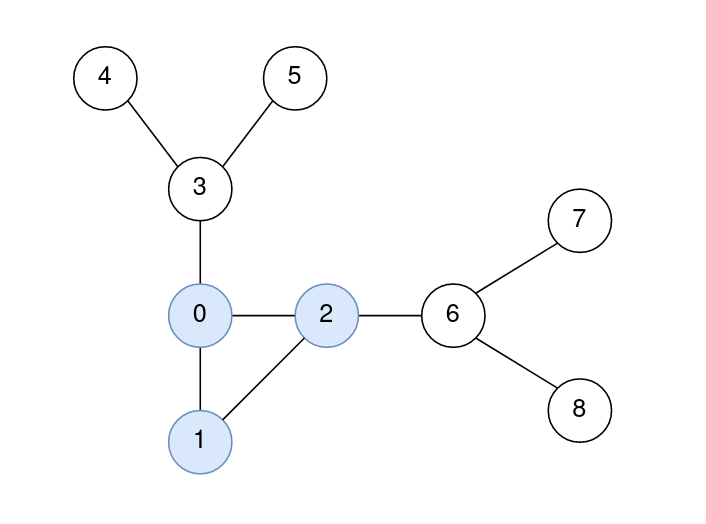
Input: n = 9, edges = [[0,1],[1,2],[0,2],[2,6],[6,7],[6,8],[0,3],[3,4],[3,5]]
Output: [0,0,0,1,2,2,1,2,2]
Explanation:
The nodes 0, 1, and 2 form the cycle.
The distance from 0 to 0 is 0.
The distance from 1 to 1 is 0.
The distance from 2 to 2 is 0.
The distance from 3 to 1 is 1.
The distance from 4 to 1 is 2.
The distance from 5 to 1 is 2.
The distance from 6 to 2 is 1.
The distance from 7 to 2 is 2.
The distance from 8 to 2 is 2.

Constraints:

3 <= n <= 10⁵
edges.length == n
edges[i].length == 2
0 <= node1_i, node2_i <= n - 1
node1_i != node2_i
The graph is connected.
The graph has exactly one cycle.
There is at most one edge between any pair of vertices.

Solutions

Solution 1: Topological Sorting

We can first convert the edges in \(edges\) into an adjacency list \(g\), where \(g[i]\) represents all adjacent nodes of node \(i\), represented as a set.

Next, we delete nodes layer by layer from the outside to the inside until only a cycle remains. The specific method is as follows:

We first find all nodes with a degree of \(1\) and remove these nodes from the graph. If after deletion, the degree of its adjacent node becomes \(1\), then we add it to the queue \(q\). During this process, we record all deleted nodes in order as \(seq\); and we use an array \(f\) to record the adjacent node of each node that is closer to the cycle, i.e., \(f[i]\) represents the adjacent node of node \(i\) that is closer to the cycle.

Finally, we initialize an answer array \(ans\) of length \(n\), where \(ans[i]\) represents the minimum distance from node \(i\) to any node in the cycle, initially \(ans[i] = 0\). Then, we start traversing from the end of \(seq\). For each node \(i\), we can get the value of \(ans[i]\) from its adjacent node \(f[i]\), i.e., \(ans[i] = ans[f[i]] + 1\).

After the traversal, return the answer array \(ans\).

The time complexity is \(O(n)\), and the space complexity is \(O(n)\). Here, \(n\) is the number of nodes.

Similar problems:

2603. Collect Coins in a Tree

Python3JavaC++GoTypeScript

class Solution:
    def distanceToCycle(self, n: int, edges: List[List[int]]) -> List[int]:
        g = defaultdict(set)
        for a, b in edges:
            g[a].add(b)
            g[b].add(a)
        q = deque(i for i in range(n) if len(g[i]) == 1)
        f = [0] * n
        seq = []
        while q:
            i = q.popleft()
            seq.append(i)
            for j in g[i]:
                g[j].remove(i)
                f[i] = j
                if len(g[j]) == 1:
                    q.append(j)
            g[i].clear()
        ans = [0] * n
        for i in seq[::-1]:
            ans[i] = ans[f[i]] + 1
        return ans

class Solution {
    public int[] distanceToCycle(int n, int[][] edges) {
        Set<Integer>[] g = new Set[n];
        Arrays.setAll(g, k -> new HashSet<>());
        for (var e : edges) {
            int a = e[0], b = e[1];
            g[a].add(b);
            g[b].add(a);
        }
        Deque<Integer> q = new ArrayDeque<>();
        for (int i = 0; i < n; ++i) {
            if (g[i].size() == 1) {
                q.offer(i);
            }
        }
        int[] f = new int[n];
        Deque<Integer> seq = new ArrayDeque<>();
        while (!q.isEmpty()) {
            int i = q.poll();
            seq.push(i);
            for (int j : g[i]) {
                g[j].remove(i);
                f[i] = j;
                if (g[j].size() == 1) {
                    q.offer(j);
                }
            }
        }
        int[] ans = new int[n];
        while (!seq.isEmpty()) {
            int i = seq.pop();
            ans[i] = ans[f[i]] + 1;
        }
        return ans;
    }
}

class Solution {
public:
    vector<int> distanceToCycle(int n, vector<vector<int>>& edges) {
        unordered_set<int> g[n];
        for (auto& e : edges) {
            int a = e[0], b = e[1];
            g[a].insert(b);
            g[b].insert(a);
        }
        queue<int> q;
        for (int i = 0; i < n; ++i) {
            if (g[i].size() == 1) {
                q.push(i);
            }
        }
        int f[n];
        int seq[n];
        int k = 0;
        while (!q.empty()) {
            int i = q.front();
            q.pop();
            seq[k++] = i;
            for (int j : g[i]) {
                g[j].erase(i);
                f[i] = j;
                if (g[j].size() == 1) {
                    q.push(j);
                }
            }
            g[i].clear();
        }
        vector<int> ans(n);
        for (; k; --k) {
            int i = seq[k - 1];
            ans[i] = ans[f[i]] + 1;
        }
        return ans;
    }
};

func distanceToCycle(n int, edges [][]int) []int {
    g := make([]map[int]bool, n)
    for i := range g {
        g[i] = map[int]bool{}
    }
    for _, e := range edges {
        a, b := e[0], e[1]
        g[a][b] = true
        g[b][a] = true
    }
    q := []int{}
    for i := 0; i < n; i++ {
        if len(g[i]) == 1 {
            q = append(q, i)
        }
    }
    f := make([]int, n)
    seq := []int{}
    for len(q) > 0 {
        i := q[0]
        q = q[1:]
        seq = append(seq, i)
        for j := range g[i] {
            delete(g[j], i)
            f[i] = j
            if len(g[j]) == 1 {
                q = append(q, j)
            }
        }
        g[i] = map[int]bool{}
    }
    ans := make([]int, n)
    for k := len(seq) - 1; k >= 0; k-- {
        i := seq[k]
        ans[i] = ans[f[i]] + 1
    }
    return ans
}

function distanceToCycle(n: number, edges: number[][]): number[] {
    const g: Set<number>[] = new Array(n).fill(0).map(() => new Set<number>());
    for (const [a, b] of edges) {
        g[a].add(b);
        g[b].add(a);
    }
    const q: number[] = [];
    for (let i = 0; i < n; ++i) {
        if (g[i].size === 1) {
            q.push(i);
        }
    }
    const f: number[] = Array(n).fill(0);
    const seq: number[] = [];
    while (q.length) {
        const i = q.pop()!;
        seq.push(i);
        for (const j of g[i]) {
            g[j].delete(i);
            f[i] = j;
            if (g[j].size === 1) {
                q.push(j);
            }
        }
        g[i].clear();
    }
    const ans: number[] = Array(n).fill(0);
    while (seq.length) {
        const i = seq.pop()!;
        ans[i] = ans[f[i]] + 1;
    }
    return ans;
}

2204. Distance to a Cycle in Undirected Graph 🔒

Description

Solutions

Solution 1: Topological Sorting

Comments