Array
Ordered Set
Segment Tree
Description
There is a long and thin painting that can be represented by a number line. You are given a 0-indexed 2D integer array paint of length n, where paint[i] = [starti , endi ]. This means that on the ith day you need to paint the area between starti and endi .
Painting the same area multiple times will create an uneven painting so you only want to paint each area of the painting at most once .
Return an integer array worklog of length n, where worklog[i] is the amount of new area that you painted on the ith day.
Example 1:
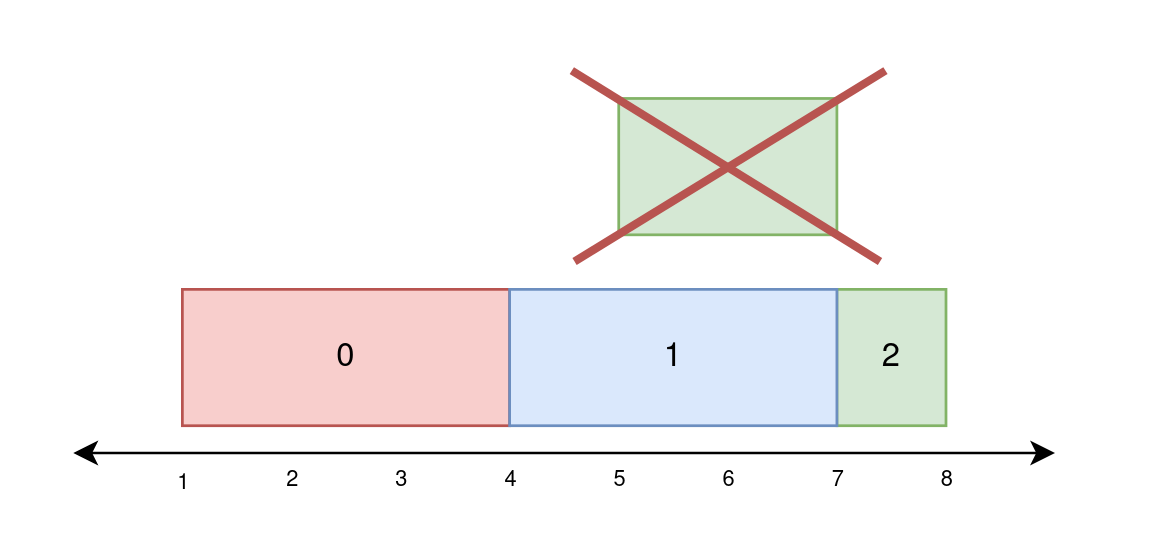
Input: paint = [[1,4],[4,7],[5,8]]
Output: [3,3,1]
Explanation:
On day 0, paint everything between 1 and 4.
The amount of new area painted on day 0 is 4 - 1 = 3.
On day 1, paint everything between 4 and 7.
The amount of new area painted on day 1 is 7 - 4 = 3.
On day 2, paint everything between 7 and 8.
Everything between 5 and 7 was already painted on day 1.
The amount of new area painted on day 2 is 8 - 7 = 1.
Example 2:
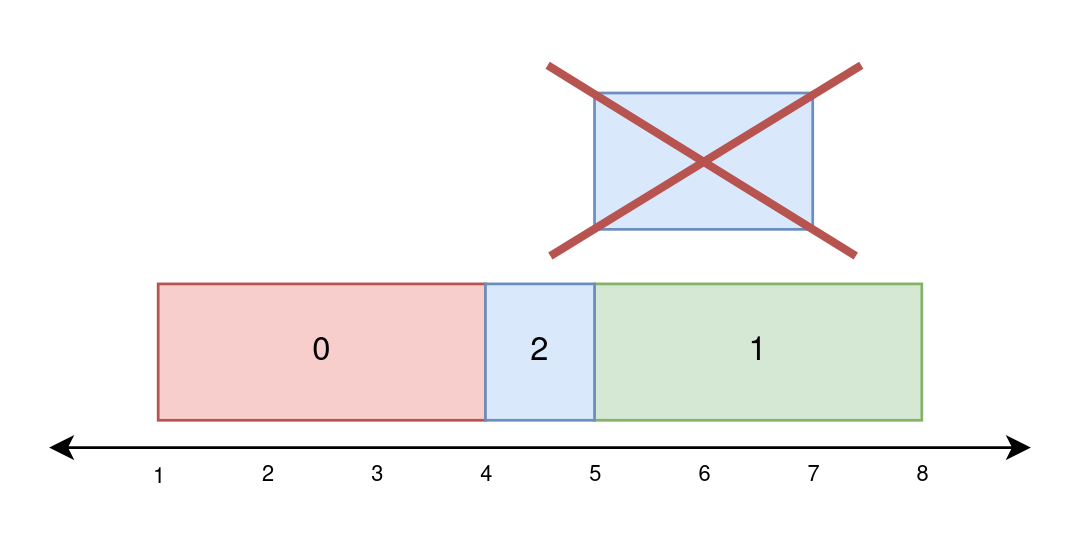
Input: paint = [[1,4],[5,8],[4,7]]
Output: [3,3,1]
Explanation:
On day 0, paint everything between 1 and 4.
The amount of new area painted on day 0 is 4 - 1 = 3.
On day 1, paint everything between 5 and 8.
The amount of new area painted on day 1 is 8 - 5 = 3.
On day 2, paint everything between 4 and 5.
Everything between 5 and 7 was already painted on day 1.
The amount of new area painted on day 2 is 5 - 4 = 1.
Example 3:
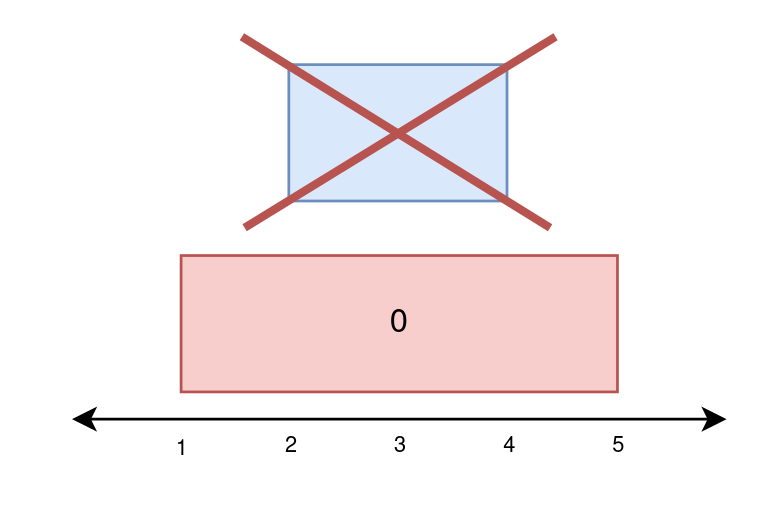
Input: paint = [[1,5],[2,4]]
Output: [4,0]
Explanation:
On day 0, paint everything between 1 and 5.
The amount of new area painted on day 0 is 5 - 1 = 4.
On day 1, paint nothing because everything between 2 and 4 was already painted on day 0.
The amount of new area painted on day 1 is 0.
Constraints:
1 <= paint.length <= 105 paint[i].length == 20 <= starti < endi <= 5 * 104
Solutions
Solution 1
Python3 Java C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73 class Node :
def __init__ ( self , l , r ):
self . left = None
self . right = None
self . l = l
self . r = r
self . mid = ( l + r ) >> 1
self . v = 0
self . add = 0
class SegmentTree :
def __init__ ( self ):
self . root = Node ( 1 , 10 ** 5 + 10 )
def modify ( self , l , r , v , node = None ):
if l > r :
return
if node is None :
node = self . root
if node . l >= l and node . r <= r :
node . v = node . r - node . l + 1
node . add = v
return
self . pushdown ( node )
if l <= node . mid :
self . modify ( l , r , v , node . left )
if r > node . mid :
self . modify ( l , r , v , node . right )
self . pushup ( node )
def query ( self , l , r , node = None ):
if l > r :
return 0
if node is None :
node = self . root
if node . l >= l and node . r <= r :
return node . v
self . pushdown ( node )
v = 0
if l <= node . mid :
v += self . query ( l , r , node . left )
if r > node . mid :
v += self . query ( l , r , node . right )
return v
def pushup ( self , node ):
node . v = node . left . v + node . right . v
def pushdown ( self , node ):
if node . left is None :
node . left = Node ( node . l , node . mid )
if node . right is None :
node . right = Node ( node . mid + 1 , node . r )
if node . add :
left , right = node . left , node . right
left . v = left . r - left . l + 1
right . v = right . r - right . l + 1
left . add = node . add
right . add = node . add
node . add = 0
class Solution :
def amountPainted ( self , paint : List [ List [ int ]]) -> List [ int ]:
tree = SegmentTree ()
ans = []
for i , ( start , end ) in enumerate ( paint ):
l , r = start + 1 , end
v = tree . query ( l , r )
ans . append ( r - l + 1 - v )
tree . modify ( l , r , 1 )
return ans
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104 class Node {
Node left ;
Node right ;
int l ;
int r ;
int mid ;
int v ;
int add ;
public Node ( int l , int r ) {
this . l = l ;
this . r = r ;
this . mid = ( l + r ) >> 1 ;
}
}
class SegmentTree {
private Node root = new Node ( 1 , 100010 );
public SegmentTree () {
}
public void modify ( int l , int r , int v ) {
modify ( l , r , v , root );
}
public void modify ( int l , int r , int v , Node node ) {
if ( l > r ) {
return ;
}
if ( node . l >= l && node . r <= r ) {
node . v = node . r - node . l + 1 ;
node . add = v ;
return ;
}
pushdown ( node );
if ( l <= node . mid ) {
modify ( l , r , v , node . left );
}
if ( r > node . mid ) {
modify ( l , r , v , node . right );
}
pushup ( node );
}
public int query ( int l , int r ) {
return query ( l , r , root );
}
public int query ( int l , int r , Node node ) {
if ( l > r ) {
return 0 ;
}
if ( node . l >= l && node . r <= r ) {
return node . v ;
}
pushdown ( node );
int v = 0 ;
if ( l <= node . mid ) {
v += query ( l , r , node . left );
}
if ( r > node . mid ) {
v += query ( l , r , node . right );
}
return v ;
}
public void pushup ( Node node ) {
node . v = node . left . v + node . right . v ;
}
public void pushdown ( Node node ) {
if ( node . left == null ) {
node . left = new Node ( node . l , node . mid );
}
if ( node . right == null ) {
node . right = new Node ( node . mid + 1 , node . r );
}
if ( node . add != 0 ) {
Node left = node . left , right = node . right ;
left . add = node . add ;
right . add = node . add ;
left . v = left . r - left . l + 1 ;
right . v = right . r - right . l + 1 ;
node . add = 0 ;
}
}
}
class Solution {
public int [] amountPainted ( int [][] paint ) {
SegmentTree tree = new SegmentTree ();
int n = paint . length ;
int [] ans = new int [ n ] ;
for ( int i = 0 ; i < n ; ++ i ) {
int l = paint [ i ][ 0 ] + 1 ;
int r = paint [ i ][ 1 ] ;
int v = tree . query ( l , r );
ans [ i ] = r - l + 1 - v ;
tree . modify ( l , r , 1 );
}
return ans ;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94 class Node {
public :
Node * left ;
Node * right ;
int l ;
int r ;
int mid ;
int v ;
int add ;
Node ( int l , int r ) {
this -> l = l ;
this -> r = r ;
this -> mid = ( l + r ) >> 1 ;
this -> left = this -> right = nullptr ;
v = add = 0 ;
}
};
class SegmentTree {
private :
Node * root ;
public :
SegmentTree () {
root = new Node ( 1 , 100010 );
}
void modify ( int l , int r , int v ) {
modify ( l , r , v , root );
}
void modify ( int l , int r , int v , Node * node ) {
if ( l > r ) return ;
if ( node -> l >= l && node -> r <= r ) {
node -> v = node -> r - node -> l + 1 ;
node -> add = v ;
return ;
}
pushdown ( node );
if ( l <= node -> mid ) modify ( l , r , v , node -> left );
if ( r > node -> mid ) modify ( l , r , v , node -> right );
pushup ( node );
}
int query ( int l , int r ) {
return query ( l , r , root );
}
int query ( int l , int r , Node * node ) {
if ( l > r ) return 0 ;
if ( node -> l >= l && node -> r <= r ) return node -> v ;
pushdown ( node );
int v = 0 ;
if ( l <= node -> mid ) v += query ( l , r , node -> left );
if ( r > node -> mid ) v += query ( l , r , node -> right );
return v ;
}
void pushup ( Node * node ) {
node -> v = node -> left -> v + node -> right -> v ;
}
void pushdown ( Node * node ) {
if ( ! node -> left ) node -> left = new Node ( node -> l , node -> mid );
if ( ! node -> right ) node -> right = new Node ( node -> mid + 1 , node -> r );
if ( node -> add ) {
Node * left = node -> left ;
Node * right = node -> right ;
left -> v = left -> r - left -> l + 1 ;
right -> v = right -> r - right -> l + 1 ;
left -> add = node -> add ;
right -> add = node -> add ;
node -> add = 0 ;
}
}
};
class Solution {
public :
vector < int > amountPainted ( vector < vector < int >>& paint ) {
int n = paint . size ();
vector < int > ans ( n );
SegmentTree * tree = new SegmentTree ();
for ( int i = 0 ; i < n ; ++ i ) {
int l = paint [ i ][ 0 ] + 1 ;
int r = paint [ i ][ 1 ];
int v = tree -> query ( l , r );
ans [ i ] = r - l + 1 - v ;
tree -> modify ( l , r , 1 );
}
return ans ;
}
};
GitHub