2152. Minimum Number of Lines to Cover Points 🔒

Description

You are given an array points where points[i] = [xi, yi] represents a point on an X-Y plane.

Straight lines are going to be added to the X-Y plane, such that every point is covered by at least one line.

Return the minimum number of straight lines needed to cover all the points.

 

Example 1:

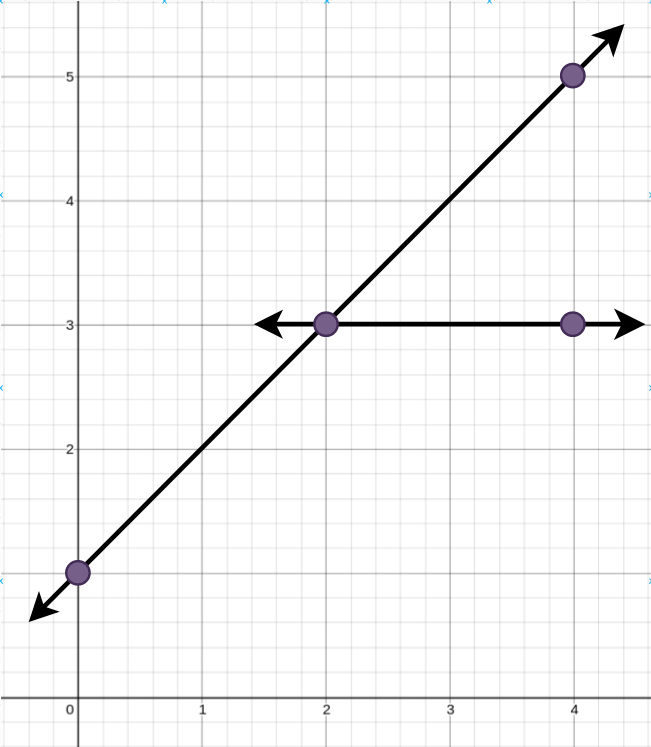
Input: points = [[0,1],[2,3],[4,5],[4,3]]
Output: 2
Explanation: The minimum number of straight lines needed is two. One possible solution is to add:
- One line connecting the point at (0, 1) to the point at (4, 5).
- Another line connecting the point at (2, 3) to the point at (4, 3).

Example 2:

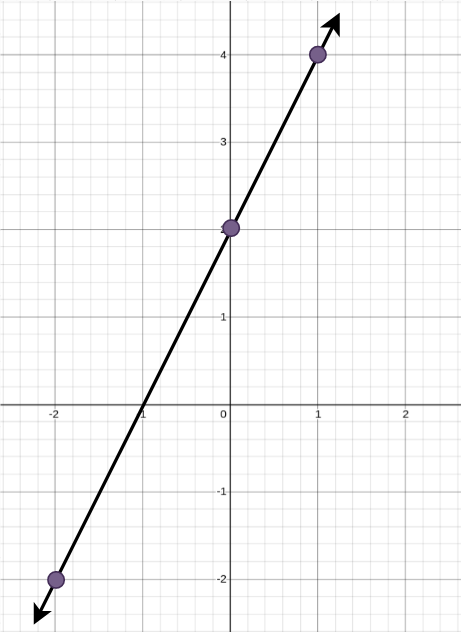
Input: points = [[0,2],[-2,-2],[1,4]]
Output: 1
Explanation: The minimum number of straight lines needed is one. The only solution is to add:
- One line connecting the point at (-2, -2) to the point at (1, 4).

 

Constraints:

• 1 <= points.length <= 10
• points[i].length == 2
• -100 <= xi, yi <= 100
• All the points are unique.

Solutions

Solution 1

Python3JavaC++Go

class Solution:
    def minimumLines(self, points: List[List[int]]) -> int:
        def check(i, j, k):
            x1, y1 = points[i]
            x2, y2 = points[j]
            x3, y3 = points[k]
            return (x2 - x1) * (y3 - y1) == (x3 - x1) * (y2 - y1)

        @cache
        def dfs(state):
            if state == (1 << n) - 1:
                return 0
            ans = inf
            for i in range(n):
                if not (state >> i & 1):
                    for j in range(i + 1, n):
                        nxt = state | 1 << i | 1 << j
                        for k in range(j + 1, n):
                            if not (nxt >> k & 1) and check(i, j, k):
                                nxt |= 1 << k
                        ans = min(ans, dfs(nxt) + 1)
                    if i == n - 1:
                        ans = min(ans, dfs(state | 1 << i) + 1)
            return ans

        n = len(points)
        return dfs(0)

class Solution {
    private int[] f;
    private int[][] points;
    private int n;

    public int minimumLines(int[][] points) {
        n = points.length;
        this.points = points;
        f = new int[1 << n];
        return dfs(0);
    }

    private int dfs(int state) {
        if (state == (1 << n) - 1) {
            return 0;
        }
        if (f[state] != 0) {
            return f[state];
        }
        int ans = 1 << 30;
        for (int i = 0; i < n; ++i) {
            if (((state >> i) & 1) == 0) {
                for (int j = i + 1; j < n; ++j) {
                    int nxt = state | 1 << i | 1 << j;
                    for (int k = j + 1; k < n; ++k) {
                        if (((state >> k) & 1) == 0 && check(i, j, k)) {
                            nxt |= 1 << k;
                        }
                    }
                    ans = Math.min(ans, dfs(nxt) + 1);
                }
                if (i == n - 1) {
                    ans = Math.min(ans, dfs(state | 1 << i) + 1);
                }
            }
        }
        return f[state] = ans;
    }

    private boolean check(int i, int j, int k) {
        int x1 = points[i][0], y1 = points[i][1];
        int x2 = points[j][0], y2 = points[j][1];
        int x3 = points[k][0], y3 = points[k][1];
        return (x2 - x1) * (y3 - y1) == (x3 - x1) * (y2 - y1);
    }
}

class Solution {
public:
    int minimumLines(vector<vector<int>>& points) {
        auto check = [&](int i, int j, int k) {
            int x1 = points[i][0], y1 = points[i][1];
            int x2 = points[j][0], y2 = points[j][1];
            int x3 = points[k][0], y3 = points[k][1];
            return (x2 - x1) * (y3 - y1) == (x3 - x1) * (y2 - y1);
        };
        int n = points.size();
        int f[1 << n];
        memset(f, 0, sizeof f);
        function<int(int)> dfs = [&](int state) -> int {
            if (state == (1 << n) - 1) return 0;
            if (f[state]) return f[state];
            int ans = 1 << 30;
            for (int i = 0; i < n; ++i) {
                if (!(state >> i & 1)) {
                    for (int j = i + 1; j < n; ++j) {
                        int nxt = state | 1 << i | 1 << j;
                        for (int k = j + 1; k < n; ++k) {
                            if (!(nxt >> k & 1) && check(i, j, k)) {
                                nxt |= 1 << k;
                            }
                        }
                        ans = min(ans, dfs(nxt) + 1);
                    }
                    if (i == n - 1) {
                        ans = min(ans, dfs(state | 1 << i) + 1);
                    }
                }
            }
            return f[state] = ans;
        };
        return dfs(0);
    }
};

func minimumLines(points [][]int) int {
    check := func(i, j, k int) bool {
        x1, y1 := points[i][0], points[i][1]
        x2, y2 := points[j][0], points[j][1]
        x3, y3 := points[k][0], points[k][1]
        return (x2-x1)*(y3-y1) == (x3-x1)*(y2-y1)
    }
    n := len(points)
    f := make([]int, 1<<n)
    var dfs func(int) int
    dfs = func(state int) int {
        if state == (1<<n)-1 {
            return 0
        }
        if f[state] > 0 {
            return f[state]
        }
        ans := 1 << 30
        for i := 0; i < n; i++ {
            if (state >> i & 1) == 0 {
                for j := i + 1; j < n; j++ {
                    nxt := state | 1<<i | 1<<j
                    for k := j + 1; k < n; k++ {
                        if (nxt>>k&1) == 0 && check(i, j, k) {
                            nxt |= 1 << k
                        }
                    }
                    ans = min(ans, dfs(nxt)+1)
                }
                if i == n-1 {
                    ans = min(ans, dfs(state|1<<i)+1)
                }
            }
        }
        f[state] = ans
        return ans
    }
    return dfs(0)
}

Comments