Skip to content

2141. Maximum Running Time of N Computers

Description

You have n computers. You are given the integer n and a 0-indexed integer array batteries where the ith battery can run a computer for batteries[i] minutes. You are interested in running all n computers simultaneously using the given batteries.

Initially, you can insert at most one battery into each computer. After that and at any integer time moment, you can remove a battery from a computer and insert another battery any number of times. The inserted battery can be a totally new battery or a battery from another computer. You may assume that the removing and inserting processes take no time.

Note that the batteries cannot be recharged.

Return the maximum number of minutes you can run all the n computers simultaneously.

 

Example 1:

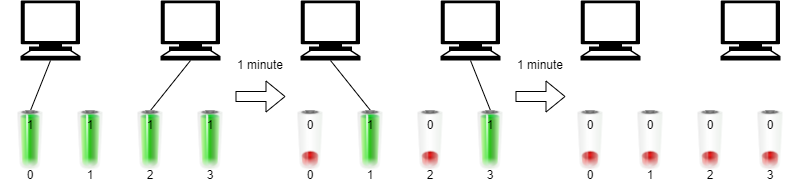
Input: n = 2, batteries = [3,3,3]
Output: 4
Explanation: 
Initially, insert battery 0 into the first computer and battery 1 into the second computer.
After two minutes, remove battery 1 from the second computer and insert battery 2 instead. Note that battery 1 can still run for one minute.
At the end of the third minute, battery 0 is drained, and you need to remove it from the first computer and insert battery 1 instead.
By the end of the fourth minute, battery 1 is also drained, and the first computer is no longer running.
We can run the two computers simultaneously for at most 4 minutes, so we return 4.

Example 2:

Input: n = 2, batteries = [1,1,1,1]
Output: 2
Explanation: 
Initially, insert battery 0 into the first computer and battery 2 into the second computer. 
After one minute, battery 0 and battery 2 are drained so you need to remove them and insert battery 1 into the first computer and battery 3 into the second computer. 
After another minute, battery 1 and battery 3 are also drained so the first and second computers are no longer running.
We can run the two computers simultaneously for at most 2 minutes, so we return 2.

 

Constraints:

  • 1 <= n <= batteries.length <= 105
  • 1 <= batteries[i] <= 109

Solutions

We notice that if we can run $n$ computers simultaneously for $t$ minutes, then we can also run $n$ computers simultaneously for $t' \le t$ minutes, which shows monotonicity. Therefore, we can use the binary search method to find the maximum $t$.

We define the left boundary of the binary search as $l=0$ and the right boundary as $r=\sum_{i=0}^{n-1} batteries[i]$. During each binary search iteration, we use a variable $mid$ to represent the current middle value, i.e., $mid = (l + r + 1) >> 1$. We check if there exists a scheme that allows $n$ computers to run simultaneously for $mid$ minutes. If such a scheme exists, then we update $l$ to $mid$; otherwise, we update $r$ to $mid - 1$. Finally, we return $l$ as the answer.

The problem is transformed into how to determine if there exists a scheme that allows $n$ computers to run simultaneously for $mid$ minutes. If a battery can run for more minutes than $mid$, since the computers run simultaneously for $mid$ minutes and a battery can only power one computer at a time, we can only use this battery for $mid$ minutes. If a battery can run for minutes less than or equal to $mid$, we can use all the power of this battery. Therefore, we calculate the total minutes $s$ that all batteries can power, and if $s \ge n \times mid$, then we can make $n$ computers run simultaneously for $mid$ minutes.

The time complexity is $O(n \times \log M)$, where $M$ is the total power of all batteries, and the space complexity is $O(1)$.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
class Solution:
    def maxRunTime(self, n: int, batteries: List[int]) -> int:
        l, r = 0, sum(batteries)
        while l < r:
            mid = (l + r + 1) >> 1
            if sum(min(x, mid) for x in batteries) >= n * mid:
                l = mid
            else:
                r = mid - 1
        return l

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public long maxRunTime(int n, int[] batteries) {
        long l = 0, r = 0;
        for (int x : batteries) {
            r += x;
        }
        while (l < r) {
            long mid = (l + r + 1) >> 1;
            long s = 0;
            for (int x : batteries) {
                s += Math.min(mid, x);
            }
            if (s >= n * mid) {
                l = mid;
            } else {
                r = mid - 1;
            }
        }
        return l;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    long long maxRunTime(int n, vector<int>& batteries) {
        long long l = 0, r = 0;
        for (int x : batteries) {
            r += x;
        }
        while (l < r) {
            long long mid = (l + r + 1) >> 1;
            long long s = 0;
            for (int x : batteries) {
                s += min(1LL * x, mid);
            }
            if (s >= n * mid) {
                l = mid;
            } else {
                r = mid - 1;
            }
        }
        return l;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
func maxRunTime(n int, batteries []int) int64 {
    l, r := 0, 0
    for _, x := range batteries {
        r += x
    }
    for l < r {
        mid := (l + r + 1) >> 1
        s := 0
        for _, x := range batteries {
            s += min(x, mid)
        }
        if s >= n*mid {
            l = mid
        } else {
            r = mid - 1
        }
    }
    return int64(l)
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
function maxRunTime(n: number, batteries: number[]): number {
    let l = 0n;
    let r = 0n;
    for (const x of batteries) {
        r += BigInt(x);
    }
    while (l < r) {
        const mid = (l + r + 1n) >> 1n;
        let s = 0n;
        for (const x of batteries) {
            s += BigInt(Math.min(x, Number(mid)));
        }
        if (s >= mid * BigInt(n)) {
            l = mid;
        } else {
            r = mid - 1n;
        }
    }
    return Number(l);
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
impl Solution {
    #[allow(dead_code)]
    pub fn max_run_time(n: i32, batteries: Vec<i32>) -> i64 {
        // First sort the batteries
        let mut batteries = batteries;
        let m = batteries.len() as i32;
        batteries.sort();

        let mut extra_sum: i64 = 0;
        for i in 0..(m - n) as usize {
            extra_sum += batteries[i] as i64;
        }

        let mut i = (m - n) as usize;
        let mut cur_height = batteries[i];
        let mut ret = cur_height as i64;
        while extra_sum != 0 {
            if i + 1 == (m as usize) {
                assert!(cur_height == *batteries.last().unwrap());
                ret += extra_sum / (n as i64);
                break;
            }

            if batteries[i] == batteries[i + 1] {
                i += 1;
                continue;
            }

            let diff = extra_sum / ((i - ((m - n) as usize) + 1) as i64);

            if (cur_height as i64) + diff <= (batteries[i + 1] as i64) {
                ret = (cur_height as i64) + diff;
                break;
            } else {
                extra_sum -= ((batteries[i + 1] - batteries[i]) as i64)
                    * ((i - ((m - n) as usize) + 1) as i64);
                ret = batteries[i + 1] as i64;
            }

            i += 1;
            if i != (m as usize) {
                cur_height = batteries[i];
            }
        }

        ret
    }
}

Comments