2125. Number of Laser Beams in a Bank

Description

Anti-theft security devices are activated inside a bank. You are given a 0-indexed binary string array bank representing the floor plan of the bank, which is an m x n 2D matrix. bank[i] represents the ith row, consisting of '0's and '1's. '0' means the cell is empty, while'1' means the cell has a security device.

There is one laser beam between any two security devices if both conditions are met:

• The two devices are located on two different rows: r1 and r2, where r1 < r2.
• For each row i where r1 < i < r2, there are no security devices in the ith row.

Laser beams are independent, i.e., one beam does not interfere nor join with another.

Return the total number of laser beams in the bank.

 

Example 1:

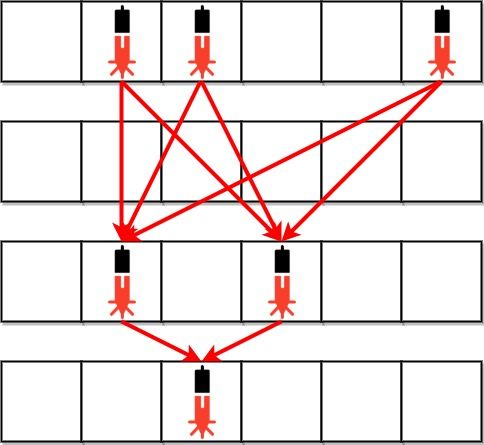
Input: bank = ["011001","000000","010100","001000"]
Output: 8
Explanation: Between each of the following device pairs, there is one beam. In total, there are 8 beams:
 * bank[0][1] -- bank[2][1]
 * bank[0][1] -- bank[2][3]
 * bank[0][2] -- bank[2][1]
 * bank[0][2] -- bank[2][3]
 * bank[0][5] -- bank[2][1]
 * bank[0][5] -- bank[2][3]
 * bank[2][1] -- bank[3][2]
 * bank[2][3] -- bank[3][2]
Note that there is no beam between any device on the 0th row with any on the 3rd row.
This is because the 2nd row contains security devices, which breaks the second condition.

Example 2:

Input: bank = ["000","111","000"]
Output: 0
Explanation: There does not exist two devices located on two different rows.

 

Constraints:

• m == bank.length
• n == bank[i].length
• 1 <= m, n <= 500
• bank[i][j] is either '0' or '1'.

Solutions

Solution 1: Row by Row Counting

We can count the number of safety devices row by row. If the current row does not have any safety devices, we skip it. Otherwise, we multiply the number of safety devices in the current row by the number of safety devices in the previous row, and add it to the answer. Then we update the number of safety devices in the previous row to be the number of safety devices in the current row.

The time complexity is $O(m \times n)$, where $m$ and $n$ are the number of rows and columns, respectively. The space complexity is $O(1)$.

Python3JavaC++GoTypeScriptRustC

class Solution:
    def numberOfBeams(self, bank: List[str]) -> int:
        ans = pre = 0
        for row in bank:
            if (cur := row.count("1")) > 0:
                ans += pre * cur
                pre = cur
        return ans

class Solution {
    public int numberOfBeams(String[] bank) {
        int ans = 0, pre = 0;
        for (String row : bank) {
            int cur = 0;
            for (int i = 0; i < row.length(); ++i) {
                cur += row.charAt(i) - '0';
            }
            if (cur > 0) {
                ans += pre * cur;
                pre = cur;
            }
        }
        return ans;
    }
}

class Solution {
public:
    int numberOfBeams(vector<string>& bank) {
        int ans = 0, pre = 0;
        for (auto& row : bank) {
            int cur = count(row.begin(), row.end(), '1');
            if (cur) {
                ans += pre * cur;
                pre = cur;
            }
        }
        return ans;
    }
};

func numberOfBeams(bank []string) (ans int) {
    pre := 0
    for _, row := range bank {
        if cur := strings.Count(row, "1"); cur > 0 {
            ans += pre * cur
            pre = cur
        }
    }
    return
}

function numberOfBeams(bank: string[]): number {
    let [ans, pre] = [0, 0];
    for (const row of bank) {
        const cur = row.split('1').length - 1;
        if (cur) {
            ans += pre * cur;
            pre = cur;
        }
    }
    return ans;
}

impl Solution {
    pub fn number_of_beams(bank: Vec<String>) -> i32 {
        let mut ans = 0;
        let mut pre = 0;
        for row in bank {
            let cur = row
                .chars()
                .filter(|&c| c == '1')
                .count() as i32;
            if cur > 0 {
                ans += pre * cur;
                pre = cur;
            }
        }
        ans
    }
}

int numberOfBeams(char** bank, int bankSize) {
    int ans = 0, pre = 0;
    for (int i = 0; i < bankSize; ++i) {
        int cur = 0;
        for (int j = 0; bank[i][j] != '\0'; ++j) {
            if (bank[i][j] == '1') {
                cur++;
            }
        }
        if (cur) {
            ans += pre * cur;
            pre = cur;
        }
    }
    return ans;
}

Comments