Skip to content

2033. Minimum Operations to Make a Uni-Value Grid

Description

You are given a 2D integer grid of size m x n and an integer x. In one operation, you can add x to or subtract x from any element in the grid.

A uni-value grid is a grid where all the elements of it are equal.

Return the minimum number of operations to make the grid uni-value. If it is not possible, return -1.

 

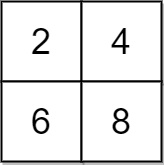
Example 1:

Input: grid = [[2,4],[6,8]], x = 2
Output: 4
Explanation: We can make every element equal to 4 by doing the following: 
- Add x to 2 once.
- Subtract x from 6 once.
- Subtract x from 8 twice.
A total of 4 operations were used.

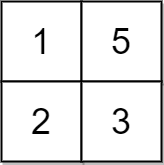
Example 2:

Input: grid = [[1,5],[2,3]], x = 1
Output: 5
Explanation: We can make every element equal to 3.

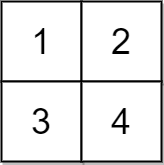
Example 3:

Input: grid = [[1,2],[3,4]], x = 2
Output: -1
Explanation: It is impossible to make every element equal.

 

Constraints:

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 105
  • 1 <= m * n <= 105
  • 1 <= x, grid[i][j] <= 104

Solutions

Solution 1: Greedy

Firstly, to make the grid a single-value grid, the remainder of all elements of the grid with \(x\) must be the same.

Therefore, we can first traverse the grid to check whether the remainder of all elements with \(x\) is the same. If not, return \(-1\). Otherwise, we put all elements into an array, sort the array, take the median, then traverse the array, calculate the difference between each element and the median, divide it by \(x\), and add all the differences to get the answer.

The time complexity is \(O((m \times n) \times \log (m \times n))\), and the space complexity is \(O(m \times n)\). Here, \(m\) and \(n\) are the number of rows and columns of the grid, respectively.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
class Solution:
    def minOperations(self, grid: List[List[int]], x: int) -> int:
        nums = []
        mod = grid[0][0] % x
        for row in grid:
            for v in row:
                if v % x != mod:
                    return -1
                nums.append(v)
        nums.sort()
        mid = nums[len(nums) >> 1]
        return sum(abs(v - mid) // x for v in nums)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public int minOperations(int[][] grid, int x) {
        int m = grid.length, n = grid[0].length;
        int[] nums = new int[m * n];
        int mod = grid[0][0] % x;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] % x != mod) {
                    return -1;
                }
                nums[i * n + j] = grid[i][j];
            }
        }
        Arrays.sort(nums);
        int mid = nums[nums.length >> 1];
        int ans = 0;
        for (int v : nums) {
            ans += Math.abs(v - mid) / x;
        }
        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    int minOperations(vector<vector<int>>& grid, int x) {
        int m = grid.size(), n = grid[0].size();
        int mod = grid[0][0] % x;
        int nums[m * n];
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] % x != mod) {
                    return -1;
                }
                nums[i * n + j] = grid[i][j];
            }
        }
        sort(nums, nums + m * n);
        int mid = nums[(m * n) >> 1];
        int ans = 0;
        for (int v : nums) {
            ans += abs(v - mid) / x;
        }
        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
func minOperations(grid [][]int, x int) int {
    mod := grid[0][0] % x
    nums := []int{}
    for _, row := range grid {
        for _, v := range row {
            if v%x != mod {
                return -1
            }
            nums = append(nums, v)
        }
    }
    sort.Ints(nums)
    mid := nums[len(nums)>>1]
    ans := 0
    for _, v := range nums {
        ans += abs(v-mid) / x
    }
    return ans
}

func abs(x int) int {
    if x < 0 {
        return -x
    }
    return x
}

Comments