Skip to content

2018. Check if Word Can Be Placed In Crossword

Description

You are given an m x n matrix board, representing the current state of a crossword puzzle. The crossword contains lowercase English letters (from solved words), ' ' to represent any empty cells, and '#' to represent any blocked cells.

A word can be placed horizontally (left to right or right to left) or vertically (top to bottom or bottom to top) in the board if:

  • It does not occupy a cell containing the character '#'.
  • The cell each letter is placed in must either be ' ' (empty) or match the letter already on the board.
  • There must not be any empty cells ' ' or other lowercase letters directly left or right of the word if the word was placed horizontally.
  • There must not be any empty cells ' ' or other lowercase letters directly above or below the word if the word was placed vertically.

Given a string word, return true if word can be placed in board, or false otherwise.

 

Example 1:

Input: board = [["#", " ", "#"], [" ", " ", "#"], ["#", "c", " "]], word = "abc"
Output: true
Explanation: The word "abc" can be placed as shown above (top to bottom).

Example 2:

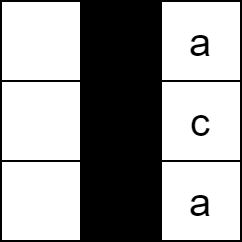
Input: board = [[" ", "#", "a"], [" ", "#", "c"], [" ", "#", "a"]], word = "ac"
Output: false
Explanation: It is impossible to place the word because there will always be a space/letter above or below it.

Example 3:

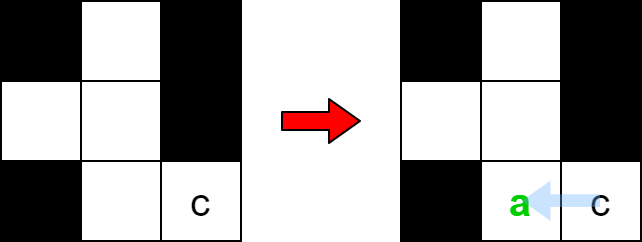
Input: board = [["#", " ", "#"], [" ", " ", "#"], ["#", " ", "c"]], word = "ca"
Output: true
Explanation: The word "ca" can be placed as shown above (right to left).

 

Constraints:

  • m == board.length
  • n == board[i].length
  • 1 <= m * n <= 2 * 105
  • board[i][j] will be ' ', '#', or a lowercase English letter.
  • 1 <= word.length <= max(m, n)
  • word will contain only lowercase English letters.

Solutions

Solution 1: Enumeration

We can enumerate each position $(i, j)$ in the matrix, and judge whether we can place the word word from left to right or from right to left, or from top to bottom or from bottom to top, starting from this position.

The following conditions must be met for this position to be used as a starting point:

  1. If the word word is to be placed from left to right, then this position must be the left boundary, or the cell board[i][j - 1] to the left of this position is '#'.
  2. If the word word is to be placed from right to left, then this position must be the right boundary, or the cell board[i][j + 1] to the right of this position is '#'.
  3. If the word word is to be placed from top to bottom, then this position must be the upper boundary, or the cell board[i - 1][j] above this position is '#'.
  4. If the word word is to be placed from bottom to top, then this position must be the lower boundary, or the cell board[i + 1][j] below this position is '#'.

Under the above conditions, we can start from this position and judge whether the word word can be placed. We design a function $check(i, j, a, b)$, which represents whether it is legal to place the word word from the position $(i, j)$ in the direction $(a, b)$. If it is legal, return true, otherwise return false.

The implementation of the function $check(i, j, a, b)$ is as follows:

We first get the other boundary position $(x, y)$ in the current direction, i.e., $(x, y) = (i + a \times k, j + b \times k)$, where $k$ is the length of the word word. If $(x, y)$ is in the matrix and the cell at $(x, y)$ is not '#', it means that the other boundary position in the current direction is not '#', so the word word cannot be placed, and false is returned.

Otherwise, we start from the position $(i, j)$ and traverse the word word in the direction $(a, b)$. If we encounter a cell board[i][j] that is not a space or not the current character of the word word, it means that the word word cannot be placed, and false is returned. If the word word is traversed, it means that the word word can be placed, and true is returned.

The time complexity is $O(m \times n)$, and the space complexity is $O(1)$. Here, $m$ and $n$ are the number of rows and columns in the matrix, respectively.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution:
    def placeWordInCrossword(self, board: List[List[str]], word: str) -> bool:
        def check(i, j, a, b):
            x, y = i + a * k, j + b * k
            if 0 <= x < m and 0 <= y < n and board[x][y] != '#':
                return False
            for c in word:
                if (
                    i < 0
                    or i >= m
                    or j < 0
                    or j >= n
                    or (board[i][j] != ' ' and board[i][j] != c)
                ):
                    return False
                i, j = i + a, j + b
            return True

        m, n = len(board), len(board[0])
        k = len(word)
        for i in range(m):
            for j in range(n):
                left_to_right = (j == 0 or board[i][j - 1] == '#') and check(i, j, 0, 1)
                right_to_left = (j == n - 1 or board[i][j + 1] == '#') and check(
                    i, j, 0, -1
                )
                up_to_down = (i == 0 or board[i - 1][j] == '#') and check(i, j, 1, 0)
                down_to_up = (i == m - 1 or board[i + 1][j] == '#') and check(
                    i, j, -1, 0
                )
                if left_to_right or right_to_left or up_to_down or down_to_up:
                    return True
        return False

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class Solution {
    private int m;
    private int n;
    private char[][] board;
    private String word;
    private int k;

    public boolean placeWordInCrossword(char[][] board, String word) {
        m = board.length;
        n = board[0].length;
        this.board = board;
        this.word = word;
        k = word.length();
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                boolean leftToRight = (j == 0 || board[i][j - 1] == '#') && check(i, j, 0, 1);
                boolean rightToLeft = (j == n - 1 || board[i][j + 1] == '#') && check(i, j, 0, -1);
                boolean upToDown = (i == 0 || board[i - 1][j] == '#') && check(i, j, 1, 0);
                boolean downToUp = (i == m - 1 || board[i + 1][j] == '#') && check(i, j, -1, 0);
                if (leftToRight || rightToLeft || upToDown || downToUp) {
                    return true;
                }
            }
        }
        return false;
    }

    private boolean check(int i, int j, int a, int b) {
        int x = i + a * k, y = j + b * k;
        if (x >= 0 && x < m && y >= 0 && y < n && board[x][y] != '#') {
            return false;
        }
        for (int p = 0; p < k; ++p) {
            if (i < 0 || i >= m || j < 0 || j >= n
                || (board[i][j] != ' ' && board[i][j] != word.charAt(p))) {
                return false;
            }
            i += a;
            j += b;
        }
        return true;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
public:
    bool placeWordInCrossword(vector<vector<char>>& board, string word) {
        int m = board.size(), n = board[0].size();
        int k = word.size();
        auto check = [&](int i, int j, int a, int b) {
            int x = i + a * k, y = j + b * k;
            if (x >= 0 && x < m && y >= 0 && y < n && board[x][y] != '#') {
                return false;
            }
            for (char& c : word) {
                if (i < 0 || i >= m || j < 0 || j >= n || (board[i][j] != ' ' && board[i][j] != c)) {
                    return false;
                }
                i += a;
                j += b;
            }
            return true;
        };
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                bool leftToRight = (j == 0 || board[i][j - 1] == '#') && check(i, j, 0, 1);
                bool rightToLeft = (j == n - 1 || board[i][j + 1] == '#') && check(i, j, 0, -1);
                bool upToDown = (i == 0 || board[i - 1][j] == '#') && check(i, j, 1, 0);
                bool downToUp = (i == m - 1 || board[i + 1][j] == '#') && check(i, j, -1, 0);
                if (leftToRight || rightToLeft || upToDown || downToUp) {
                    return true;
                }
            }
        }
        return false;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
func placeWordInCrossword(board [][]byte, word string) bool {
    m, n := len(board), len(board[0])
    k := len(word)
    check := func(i, j, a, b int) bool {
        x, y := i+a*k, j+b*k
        if x >= 0 && x < m && y >= 0 && y < n && board[x][y] != '#' {
            return false
        }
        for _, c := range word {
            if i < 0 || i >= m || j < 0 || j >= n || (board[i][j] != ' ' && board[i][j] != byte(c)) {
                return false
            }
            i, j = i+a, j+b
        }
        return true
    }
    for i := range board {
        for j := range board[i] {
            leftToRight := (j == 0 || board[i][j-1] == '#') && check(i, j, 0, 1)
            rightToLeft := (j == n-1 || board[i][j+1] == '#') && check(i, j, 0, -1)
            upToDown := (i == 0 || board[i-1][j] == '#') && check(i, j, 1, 0)
            downToUp := (i == m-1 || board[i+1][j] == '#') && check(i, j, -1, 0)
            if leftToRight || rightToLeft || upToDown || downToUp {
                return true
            }
        }
    }
    return false
}

Comments