2013. Detect Squares

Description

You are given a stream of points on the X-Y plane. Design an algorithm that:

• Adds new points from the stream into a data structure. Duplicate points are allowed and should be treated as different points.
• Given a query point, counts the number of ways to choose three points from the data structure such that the three points and the query point form an axis-aligned square with positive area.

An axis-aligned square is a square whose edges are all the same length and are either parallel or perpendicular to the x-axis and y-axis.

Implement the DetectSquares class:

• DetectSquares() Initializes the object with an empty data structure.
• void add(int[] point) Adds a new point point = [x, y] to the data structure.
• int count(int[] point) Counts the number of ways to form axis-aligned squares with point point = [x, y] as described above.

 

Example 1:

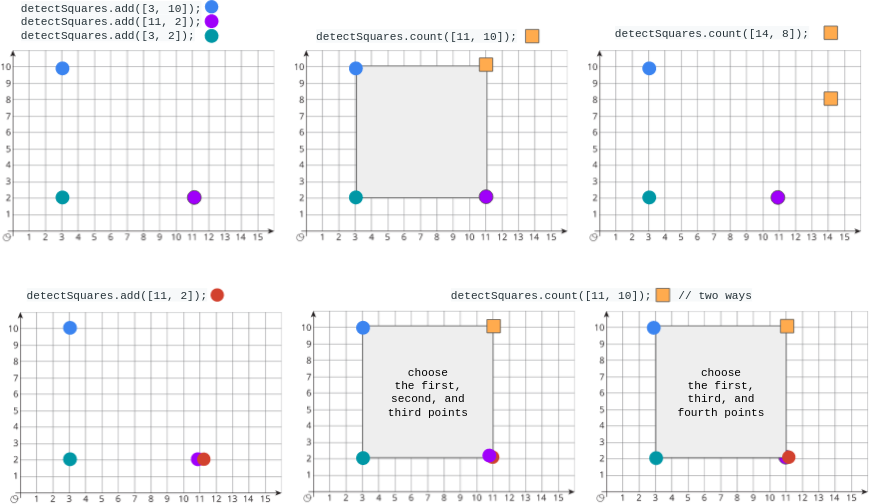
Input
["DetectSquares", "add", "add", "add", "count", "count", "add", "count"]
[[], [[3, 10]], [[11, 2]], [[3, 2]], [[11, 10]], [[14, 8]], [[11, 2]], [[11, 10]]]
Output
[null, null, null, null, 1, 0, null, 2]

Explanation
DetectSquares detectSquares = new DetectSquares();
detectSquares.add([3, 10]);
detectSquares.add([11, 2]);
detectSquares.add([3, 2]);
detectSquares.count([11, 10]); // return 1. You can choose:
// - The first, second, and third points
detectSquares.count([14, 8]); // return 0. The query point cannot form a square with any points in the data structure.
detectSquares.add([11, 2]); // Adding duplicate points is allowed.
detectSquares.count([11, 10]); // return 2. You can choose:
// - The first, second, and third points
// - The first, third, and fourth points

 

Constraints:

• point.length == 2
• 0 <= x, y <= 1000
• At most 3000 calls in total will be made to add and count.

Solutions

Solution 1: Hash Table

We can use a hash table \(cnt\) to maintain all the information of the points, where \(cnt[x][y]\) represents the count of point \((x, y)\).

When calling the \(add(x, y)\) method, we increase the value of \(cnt[x][y]\) by \(1\).

When calling the \(count(x_1, y_1)\) method, we need to get three other points to form an axis-aligned square. We can enumerate the point \((x_2, y_1)\) that is parallel to the \(x\)-axis and at a distance \(d\) from \((x_1, y_1)\). If such a point exists, based on these two points, we can determine the other two points as \((x_1, y_1 + d)\) and \((x_2, y_1 + d)\), or \((x_1, y_1 - d)\) and \((x_2, y_1 - d)\). We can add up the number of schemes for these two situations.

In terms of time complexity, the time complexity of calling the \(add(x, y)\) method is \(O(1)\), and the time complexity of calling the \(count(x_1, y_1)\) method is \(O(n)\); the space complexity is \(O(n)\). Here, \(n\) is the number of points in the data stream.

Python3JavaC++Go

class DetectSquares:
    def __init__(self):
        self.cnt = defaultdict(Counter)

    def add(self, point: List[int]) -> None:
        x, y = point
        self.cnt[x][y] += 1

    def count(self, point: List[int]) -> int:
        x1, y1 = point
        if x1 not in self.cnt:
            return 0
        ans = 0
        for x2 in self.cnt.keys():
            if x2 != x1:
                d = x2 - x1
                ans += self.cnt[x2][y1] * self.cnt[x1][y1 + d] * self.cnt[x2][y1 + d]
                ans += self.cnt[x2][y1] * self.cnt[x1][y1 - d] * self.cnt[x2][y1 - d]
        return ans


# Your DetectSquares object will be instantiated and called as such:
# obj = DetectSquares()
# obj.add(point)
# param_2 = obj.count(point)

class DetectSquares {
    private Map<Integer, Map<Integer, Integer>> cnt = new HashMap<>();

    public DetectSquares() {
    }

    public void add(int[] point) {
        int x = point[0], y = point[1];
        cnt.computeIfAbsent(x, k -> new HashMap<>()).merge(y, 1, Integer::sum);
    }

    public int count(int[] point) {
        int x1 = point[0], y1 = point[1];
        if (!cnt.containsKey(x1)) {
            return 0;
        }
        int ans = 0;
        for (var e : cnt.entrySet()) {
            int x2 = e.getKey();
            if (x2 != x1) {
                int d = x2 - x1;
                var cnt1 = cnt.get(x1);
                var cnt2 = e.getValue();
                ans += cnt2.getOrDefault(y1, 0) * cnt1.getOrDefault(y1 + d, 0)
                    * cnt2.getOrDefault(y1 + d, 0);
                ans += cnt2.getOrDefault(y1, 0) * cnt1.getOrDefault(y1 - d, 0)
                    * cnt2.getOrDefault(y1 - d, 0);
            }
        }
        return ans;
    }
}

/**
 * Your DetectSquares object will be instantiated and called as such:
 * DetectSquares obj = new DetectSquares();
 * obj.add(point);
 * int param_2 = obj.count(point);
 */

class DetectSquares {
public:
    DetectSquares() {
    }

    void add(vector<int> point) {
        int x = point[0], y = point[1];
        ++cnt[x][y];
    }

    int count(vector<int> point) {
        int x1 = point[0], y1 = point[1];
        if (!cnt.count(x1)) {
            return 0;
        }
        int ans = 0;
        for (auto& [x2, cnt2] : cnt) {
            if (x2 != x1) {
                int d = x2 - x1;
                auto& cnt1 = cnt[x1];
                ans += cnt2[y1] * cnt1[y1 + d] * cnt2[y1 + d];
                ans += cnt2[y1] * cnt1[y1 - d] * cnt2[y1 - d];
            }
        }
        return ans;
    }

private:
    unordered_map<int, unordered_map<int, int>> cnt;
};

/**
 * Your DetectSquares object will be instantiated and called as such:
 * DetectSquares* obj = new DetectSquares();
 * obj->add(point);
 * int param_2 = obj->count(point);
 */

type DetectSquares struct {
    cnt map[int]map[int]int
}

func Constructor() DetectSquares {
    return DetectSquares{map[int]map[int]int{}}
}

func (this *DetectSquares) Add(point []int) {
    x, y := point[0], point[1]
    if _, ok := this.cnt[x]; !ok {
        this.cnt[x] = map[int]int{}
    }
    this.cnt[x][y]++
}

func (this *DetectSquares) Count(point []int) (ans int) {
    x1, y1 := point[0], point[1]
    if cnt1, ok := this.cnt[x1]; ok {
        for x2, cnt2 := range this.cnt {
            if x2 != x1 {
                d := x2 - x1
                ans += cnt2[y1] * cnt1[y1+d] * cnt2[y1+d]
                ans += cnt2[y1] * cnt1[y1-d] * cnt2[y1-d]
            }
        }
    }
    return
}

/**
 * Your DetectSquares object will be instantiated and called as such:
 * obj := Constructor();
 * obj.Add(point);
 * param_2 := obj.Count(point);
 */

Comments