2003. Smallest Missing Genetic Value in Each Subtree

Description

There is a family tree rooted at 0 consisting of n nodes numbered 0 to n - 1. You are given a 0-indexed integer array parents, where parents[i] is the parent for node i. Since node 0 is the root, parents[0] == -1.

There are 10⁵ genetic values, each represented by an integer in the inclusive range [1, 10⁵]. You are given a 0-indexed integer array nums, where nums[i] is a distinct genetic value for node i.

Return an array ans of length n where ans[i] is the smallest genetic value that is missing from the subtree rooted at node i.

The subtree rooted at a node x contains node x and all of its descendant nodes.

Example 1:

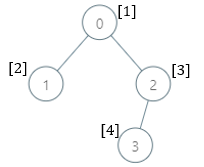
Input: parents = [-1,0,0,2], nums = [1,2,3,4]
Output: [5,1,1,1]
Explanation: The answer for each subtree is calculated as follows:
- 0: The subtree contains nodes [0,1,2,3] with values [1,2,3,4]. 5 is the smallest missing value.
- 1: The subtree contains only node 1 with value 2. 1 is the smallest missing value.
- 2: The subtree contains nodes [2,3] with values [3,4]. 1 is the smallest missing value.
- 3: The subtree contains only node 3 with value 4. 1 is the smallest missing value.

Example 2:

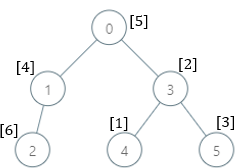
Input: parents = [-1,0,1,0,3,3], nums = [5,4,6,2,1,3]
Output: [7,1,1,4,2,1]
Explanation: The answer for each subtree is calculated as follows:
- 0: The subtree contains nodes [0,1,2,3,4,5] with values [5,4,6,2,1,3]. 7 is the smallest missing value.
- 1: The subtree contains nodes [1,2] with values [4,6]. 1 is the smallest missing value.
- 2: The subtree contains only node 2 with value 6. 1 is the smallest missing value.
- 3: The subtree contains nodes [3,4,5] with values [2,1,3]. 4 is the smallest missing value.
- 4: The subtree contains only node 4 with value 1. 2 is the smallest missing value.
- 5: The subtree contains only node 5 with value 3. 1 is the smallest missing value.

Example 3:

Input: parents = [-1,2,3,0,2,4,1], nums = [2,3,4,5,6,7,8]
Output: [1,1,1,1,1,1,1]
Explanation: The value 1 is missing from all the subtrees.

Constraints:

n == parents.length == nums.length
2 <= n <= 10⁵
0 <= parents[i] <= n - 1 for i != 0
parents[0] == -1
parents represents a valid tree.
1 <= nums[i] <= 10⁵
Each nums[i] is distinct.

Solutions

Solution 1: DFS

We notice that each node has a unique gene value, so we only need to find the node $idx$ with gene value $1$, and all nodes except for those on the path from node $idx$ to the root node $0$ have an answer of $1$.

Therefore, we initialize the answer array $ans$ to $[1,1,...,1]$, and our focus is on finding the answer for each node on the path from node $idx$ to the root node $0$.

We can start from node $idx$ and use depth-first search to mark the gene values that appear in the subtree rooted at $idx$, and record them in the array $has$. During the search process, we use an array $vis$ to mark the visited nodes to prevent repeated visits.

Next, we start from $i=2$ and keep looking for the first gene value that has not appeared, which is the answer for node $idx$. Here, $i$ is strictly increasing, because the gene values are unique, so we can always find a gene value that has not appeared in $[1,..n+1]$.

Then, we update the answer for node $idx$, i.e., $ans[idx]=i$, and update $idx$ to its parent node to continue the above process until $idx=-1$, which means we have reached the root node $0$.

Finally, we return the answer array $ans$.

The time complexity is $O(n)$, and the space complexity is $O(n)$. Here, $n$ is the number of nodes.

Python3JavaC++GoTypeScriptRust

class Solution:
    def smallestMissingValueSubtree(
        self, parents: List[int], nums: List[int]
    ) -> List[int]:
        def dfs(i: int):
            if vis[i]:
                return
            vis[i] = True
            if nums[i] < len(has):
                has[nums[i]] = True
            for j in g[i]:
                dfs(j)

        n = len(nums)
        ans = [1] * n
        g = [[] for _ in range(n)]
        idx = -1
        for i, p in enumerate(parents):
            if i:
                g[p].append(i)
            if nums[i] == 1:
                idx = i
        if idx == -1:
            return ans
        vis = [False] * n
        has = [False] * (n + 2)
        i = 2
        while idx != -1:
            dfs(idx)
            while has[i]:
                i += 1
            ans[idx] = i
            idx = parents[idx]
        return ans

class Solution {
    private List<Integer>[] g;
    private boolean[] vis;
    private boolean[] has;
    private int[] nums;

    public int[] smallestMissingValueSubtree(int[] parents, int[] nums) {
        int n = nums.length;
        this.nums = nums;
        g = new List[n];
        vis = new boolean[n];
        has = new boolean[n + 2];
        Arrays.setAll(g, i -> new ArrayList<>());
        int idx = -1;
        for (int i = 0; i < n; ++i) {
            if (i > 0) {
                g[parents[i]].add(i);
            }
            if (nums[i] == 1) {
                idx = i;
            }
        }
        int[] ans = new int[n];
        Arrays.fill(ans, 1);
        if (idx == -1) {
            return ans;
        }
        for (int i = 2; idx != -1; idx = parents[idx]) {
            dfs(idx);
            while (has[i]) {
                ++i;
            }
            ans[idx] = i;
        }
        return ans;
    }

    private void dfs(int i) {
        if (vis[i]) {
            return;
        }
        vis[i] = true;
        if (nums[i] < has.length) {
            has[nums[i]] = true;
        }
        for (int j : g[i]) {
            dfs(j);
        }
    }
}

class Solution {
public:
    vector<int> smallestMissingValueSubtree(vector<int>& parents, vector<int>& nums) {
        int n = nums.size();
        vector<int> g[n];
        bool vis[n];
        bool has[n + 2];
        memset(vis, false, sizeof(vis));
        memset(has, false, sizeof(has));
        int idx = -1;
        for (int i = 0; i < n; ++i) {
            if (i) {
                g[parents[i]].push_back(i);
            }
            if (nums[i] == 1) {
                idx = i;
            }
        }
        vector<int> ans(n, 1);
        if (idx == -1) {
            return ans;
        }
        function<void(int)> dfs = [&](int i) {
            if (vis[i]) {
                return;
            }
            vis[i] = true;
            if (nums[i] < n + 2) {
                has[nums[i]] = true;
            }
            for (int j : g[i]) {
                dfs(j);
            }
        };
        for (int i = 2; ~idx; idx = parents[idx]) {
            dfs(idx);
            while (has[i]) {
                ++i;
            }
            ans[idx] = i;
        }
        return ans;
    }
};

func smallestMissingValueSubtree(parents []int, nums []int) []int {
    n := len(nums)
    g := make([][]int, n)
    vis := make([]bool, n)
    has := make([]bool, n+2)
    idx := -1
    ans := make([]int, n)
    for i, p := range parents {
        if i > 0 {
            g[p] = append(g[p], i)
        }
        if nums[i] == 1 {
            idx = i
        }
        ans[i] = 1
    }
    if idx < 0 {
        return ans
    }
    var dfs func(int)
    dfs = func(i int) {
        if vis[i] {
            return
        }
        vis[i] = true
        if nums[i] < len(has) {
            has[nums[i]] = true
        }
        for _, j := range g[i] {
            dfs(j)
        }
    }
    for i := 2; idx != -1; idx = parents[idx] {
        dfs(idx)
        for has[i] {
            i++
        }
        ans[idx] = i
    }
    return ans
}

function smallestMissingValueSubtree(parents: number[], nums: number[]): number[] {
    const n = nums.length;
    const g: number[][] = Array.from({ length: n }, () => []);
    const vis: boolean[] = Array(n).fill(false);
    const has: boolean[] = Array(n + 2).fill(false);
    const ans: number[] = Array(n).fill(1);
    let idx = -1;
    for (let i = 0; i < n; ++i) {
        if (i) {
            g[parents[i]].push(i);
        }
        if (nums[i] === 1) {
            idx = i;
        }
    }
    if (idx === -1) {
        return ans;
    }
    const dfs = (i: number): void => {
        if (vis[i]) {
            return;
        }
        vis[i] = true;
        if (nums[i] < has.length) {
            has[nums[i]] = true;
        }
        for (const j of g[i]) {
            dfs(j);
        }
    };
    for (let i = 2; ~idx; idx = parents[idx]) {
        dfs(idx);
        while (has[i]) {
            ++i;
        }
        ans[idx] = i;
    }
    return ans;
}

impl Solution {
    pub fn smallest_missing_value_subtree(parents: Vec<i32>, nums: Vec<i32>) -> Vec<i32> {
        fn dfs(
            i: usize,
            vis: &mut Vec<bool>,
            has: &mut Vec<bool>,
            g: &Vec<Vec<usize>>,
            nums: &Vec<i32>,
        ) {
            if vis[i] {
                return;
            }
            vis[i] = true;
            if nums[i] < (has.len() as i32) {
                has[nums[i] as usize] = true;
            }
            for &j in &g[i] {
                dfs(j, vis, has, g, nums);
            }
        }

        let n = nums.len();
        let mut ans = vec![1; n];
        let mut g: Vec<Vec<usize>> = vec![vec![]; n];
        let mut idx = -1;
        for (i, &p) in parents.iter().enumerate() {
            if i > 0 {
                g[p as usize].push(i);
            }
            if nums[i] == 1 {
                idx = i as i32;
            }
        }
        if idx == -1 {
            return ans;
        }
        let mut vis = vec![false; n];
        let mut has = vec![false; (n + 2) as usize];
        let mut i = 2;
        let mut idx_mut = idx;
        while idx_mut != -1 {
            dfs(idx_mut as usize, &mut vis, &mut has, &g, &nums);
            while has[i] {
                i += 1;
            }
            ans[idx_mut as usize] = i as i32;
            idx_mut = parents[idx_mut as usize];
        }
        ans
    }
}

2003. Smallest Missing Genetic Value in Each Subtree

Description

Solutions

Solution 1: DFS

Comments